
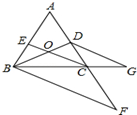
 如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB,交BD于O,且∠EOD+∠OBF=180°,∠F=∠G.试判断DG与CE是否平行,并说明理由.
如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB,交BD于O,且∠EOD+∠OBF=180°,∠F=∠G.试判断DG与CE是否平行,并说明理由. 分析 因为CE平分∠ACB,交BD于O,且∠EOD+∠OBF=180°,所以∠ECB+(180°-∠EOD)=∠DBF+∠F,即∠ECB+180°=(∠DBF+∠EOD)+∠F,又因为∠F=∠G,所以∠ECB=∠G,进而得出∠ECB=∠G,所以EC∥DG.
解答 解:∵CE平分∠ACB
∴∠ACE=∠ECB
∵在△DCO中,∠DCO+∠COD=∠ADB,∠COD+∠EOD=180°
∴∠ECB+(180°-∠EOD)=∠ADB
∵在△BDF中,∠ADB=∠DBF+∠F
又∵∠EOD+∠OBF=180°
∴∠ECB+(180°-∠EOD)=∠DBF+∠F
即∠ECB+180°=(∠DBF+∠EOD)+∠F
∴∠ECB=∠F
∵∠F=∠G
∴∠ECB=∠G
又∵G是BC的延长线上一点,∠ECB=∠G
∴EC∥DG.
点评 此题考查了平行线的性质及三角形的内角和为180°的运用.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com