
【题目】已知函数![]()
(Ⅰ)若直线![]() 且曲线
且曲线![]() 在A处的切线与
在A处的切线与![]() 在B处的切线相互平行,求a的取值范围;
在B处的切线相互平行,求a的取值范围;
(Ⅱ)设![]() 在其定义域内有两个不同的极值点
在其定义域内有两个不同的极值点![]() 且
且![]() 若不等式
若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)求出![]() 可得
可得![]() 在
在![]() 有解,转化为函数
有解,转化为函数![]() 与
与![]() 的图象在
的图象在![]() 上有交点,求出相切时
上有交点,求出相切时![]() ,利用数形结合思想可得结果;(Ⅱ)根据极值点的定义可得
,利用数形结合思想可得结果;(Ⅱ)根据极值点的定义可得![]() ,作差可得
,作差可得![]() ,
, ![]() 等价于
等价于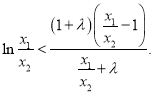 令
令![]() ,则
,则![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,讨论两种情况,分别利用导数研究函数的单调性,根据单调性可得函数最值,从而筛选符合题意的
上恒成立,讨论两种情况,分别利用导数研究函数的单调性,根据单调性可得函数最值,从而筛选符合题意的![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)依题意,函数![]() 的定义域为(0,
的定义域为(0, ![]() ),
),![]() 因为曲线
因为曲线![]() 在A处的切线与
在A处的切线与![]() 在B处的切线相互平行,所以
在B处的切线相互平行,所以![]() 有解,即方程
有解,即方程![]() 有解.
有解.
方程![]() 有解转化为函数
有解转化为函数![]() 的图像在
的图像在![]() 上有交点,
上有交点,
如图,令过原点且与函数![]() 的图像相切的直线的斜率为
的图像相切的直线的斜率为![]() ,只须
,只须![]()
令切点为![]() ,所以
,所以![]()
![]() ,所以
,所以![]()
(Ⅱ)![]()
因为![]() 在其定义域内有两个不同的极值点,所以
在其定义域内有两个不同的极值点,所以![]() 的两个根,即
的两个根,即![]()
因为![]()
![]()
![]()
![]()
![]()
![]()
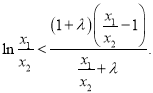
令![]() ,则
,则![]() ,由题意知,不等式
,由题意知,不等式![]() 上恒成立.
上恒成立.
令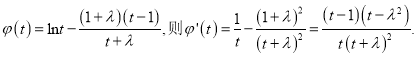
如果![]() 所以
所以![]() 上单调递增,又
上单调递增,又![]()
![]()
![]() 上恒成立,符合题意.
上恒成立,符合题意.
如果![]() 时,
时, ![]()
![]() 上单调递增,在
上单调递增,在![]() 上单调递减,又
上单调递减,又![]() 上不能恒小于0,不符合题意,舍去.
上不能恒小于0,不符合题意,舍去.
综上所述,若不等式![]() 恒成立,只须
恒成立,只须![]() .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com