考点：比的意义,圆柱的侧面积、表面积和体积,圆锥的体积
专题：立体图形的认识与计算
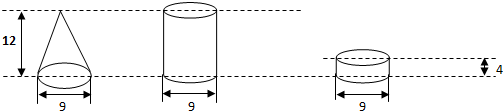
分析：根据题干可得，第一个和第二个图形等底等高，根据等底等高的圆柱的体积是圆锥的体积的3倍可得，圆锥与圆柱的体积之比是1：3，第三个圆柱与第二个圆柱等底，所以它们的体积之比就等于高的比，12：4=3：1，据此即可解答问题．
解答：
解：根据题干分析可得：因为等底等高的圆柱的体积是圆锥的体积的3倍可得，
第一个图形圆锥与第二个图形圆柱的体积之比是1：3，
第三个圆柱与第二个圆柱等底，所以第二个图形与第三个图形的体积之比是12：4=3：1，
所以三个图形的体积之比是：1：3：1．
故选：C．
点评：此题考查了圆柱与圆锥的体积公式的灵活应用．
