解:(1)根据数对表示位置的方法可得,长方形四个顶点的位置分别是(1,2)、(1,4)、(4,2)、(4,4);
(2)20-(5×20-79)÷(5+2),
=20-21÷7,
=17(题).
答:他做对了17题;
(3)

=
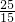
;
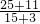
=

;
(4)根据题干可得:大平行四边形的面积×

=小平行四边形的面积×

,
所以大平行四边形的面积:小平行四边形的面积=

:

=12:8=3:2,
当大平行四边形的面积是60平方厘米时,小平行四边形的面积是:
60×2÷3=40(平方厘米);
(5)根据题干分析可得:到A公司一天能赚20+2m元,
到B公司一天能赚3m元,
m=21时,20+2m=62元,3m=63元,
所以当m>20时,到B公司应聘比较合算.
故答案为:17;
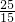
;

;3:2;40;20+2m;B.
分析:(1)数对表示位置的方法:第一个数字表示列,第二个数字表示行,由此即可解答;
(2)假设都做对,则得20×5=100分,这样就多得100-79=21分;作对一题比做错一题多得5+2=7分,也就是做错了21÷7=3道题,进而得出做对了20-3=17道题.
(3)观察题干可知,分子依次是加3、5、7、9、11,分母依次加3,由此即可解决问题;
(4)根据题干可得:大平行四边形的面积×

=小平行四边形的面积×

,由此可得:大平行四边形的面积:小平行四边形的面积=

:

=12:8=3:2,由此即可解决问题;
(5)根据题干分析可得,用m表示当天投递邮件的份数,则到A公司一天能赚20+2m元,到B公司一天能赚3m元,先计算出m=21时,20+2m=62元,3m=63元,由此即可解决问题.
点评:此题考查的知识点有:数对表示位置的方法,鸡兔同笼问题,数与形结合问题,比例的基本性质的逆应用,以及最优化问题的解决方法.

 、
、 、
、 、
、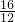 、________、________.
、________、________.
 ,相当于小平行四边形面积的
,相当于小平行四边形面积的 .大平行四边形与小平行四边形的面积比是________,如果大平行四边形的面积是60平方厘米,那么,小平行四边形的面积是________平方厘米.
.大平行四边形与小平行四边形的面积比是________,如果大平行四边形的面积是60平方厘米,那么,小平行四边形的面积是________平方厘米. =
=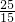 ;
;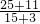 =
= ;
; =小平行四边形的面积×
=小平行四边形的面积× ,
, :
: =12:8=3:2,
=12:8=3:2,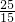 ;
; ;3:2;40;20+2m;B.
;3:2;40;20+2m;B. =小平行四边形的面积×
=小平行四边形的面积× ,由此可得:大平行四边形的面积:小平行四边形的面积=
,由此可得:大平行四边形的面积:小平行四边形的面积= :
: =12:8=3:2,由此即可解决问题;
=12:8=3:2,由此即可解决问题;

