解:1.7+3.98+
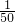
,
=1.7+(3.98+0.02),
=1.7+4,
=5.7;
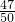
×51,
=

(50+1),
=
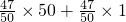
,
=47

,
=47
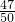
;
5.73-3
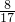
+(4.27-2
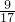
),
=5.73+4.27-(3
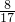
+2
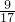
),
=10-6,
=4;
45×2.08+1.5×37.6,
=1.5×62.4+1.5×37.6,
=1.5×(62.4+37.6),
=1.5×100,
=150;
99999×77778+33333×66666,
=99999×77778+33333×(3×22222),
=99999×77778+(33333×3)×22222,
=99999×77778+99999×22222,
=99999×(77778+22222),
=99999×100000,
=9999900000;
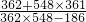
,
=(362+548×361)÷(362×548-186),
=[362+548×(362-1)]÷(362×548-186),
=[362-548+548×362]÷(362×548-186),
=(362×548-186)÷(362×548-186),
=1;
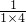
+

+
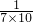
+…+
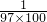
,
=

×[(1

)+(
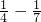
)+(

)+…+(
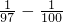
)],
=
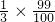
,
=
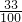
;

+

+

+

+

,
=(1-

)+(
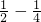
)+(

)+(
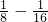
)+(
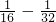
),
=1
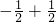
-
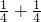
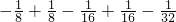
,
=1
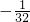
,
=
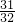
;
分析:1.7+3.98+
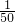
,把分数化成小数,再运用加法结合律进行简算;
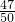
×51,把51分解为50+1,再运用乘法分配律进行简算;
5.73-3
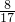
+(4.27-2
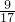
),根据加、减法的运算性质进行简算;
45×2.08+1.5×37.6,将原式转化为:1.5×62.4+1.5×37.6,再运用乘法分配律进行简算;
99999×77778+33333×66666,将666666改写成3×22222,然后用乘法结合律计算3×33333等于99999,再利用乘法分配律进行简算;
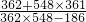
,将原式转化为:(362+548×361)÷(362×548-186)=[362+548×(362-1)]÷(362×548-186),两个括号中的数相同,商就是1.
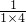
+

+
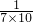
+…+
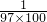
,各分数的分母中的两个数相差3,所以把原式变为原式=

×[(1

)+(
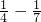
)+(

)+…+(
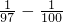
)],再进行简算;

+

+

+

+

.根据分数拆项方法进行简算;
点评:此题考查的目的是灵活运用运算定律、运算性质以及分数的拆项原理和方法进行简便计算.

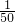
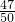 ×51
×51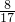 +(4.27-2
+(4.27-2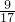 )
)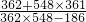
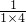 +
+ +
+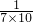 +…+
+…+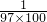
 +
+ +
+ +
+ +
+ .
.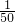 ,
,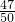 ×51,
×51, (50+1),
(50+1),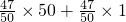 ,
, ,
,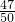 ;
;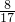 +(4.27-2
+(4.27-2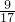 ),
),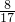 +2
+2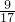 ),
),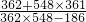 ,
,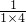 +
+ +
+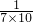 +…+
+…+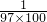 ,
, ×[(1
×[(1 )+(
)+(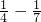 )+(
)+( )+…+(
)+…+(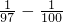 )],
)],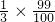 ,
,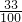 ;
; +
+ +
+ +
+ +
+ ,
, )+(
)+(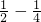 )+(
)+( )+(
)+(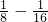 )+(
)+(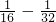 ),
),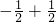 -
-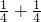
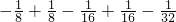 ,
,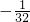 ,
,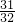 ;
;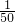 ,把分数化成小数,再运用加法结合律进行简算;
,把分数化成小数,再运用加法结合律进行简算;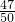 ×51,把51分解为50+1,再运用乘法分配律进行简算;
×51,把51分解为50+1,再运用乘法分配律进行简算;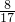 +(4.27-2
+(4.27-2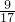 ),根据加、减法的运算性质进行简算;
),根据加、减法的运算性质进行简算;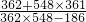 ,将原式转化为:(362+548×361)÷(362×548-186)=[362+548×(362-1)]÷(362×548-186),两个括号中的数相同,商就是1.
,将原式转化为:(362+548×361)÷(362×548-186)=[362+548×(362-1)]÷(362×548-186),两个括号中的数相同,商就是1.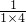 +
+ +
+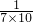 +…+
+…+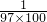 ,各分数的分母中的两个数相差3,所以把原式变为原式=
,各分数的分母中的两个数相差3,所以把原式变为原式= ×[(1
×[(1 )+(
)+(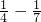 )+(
)+( )+…+(
)+…+(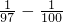 )],再进行简算;
)],再进行简算; +
+ +
+ +
+ +
+ .根据分数拆项方法进行简算;
.根据分数拆项方法进行简算;
