
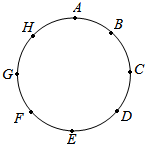
 如图,A、B、C、D、E、F、G、H是把圆形道路平均分成的8个点.甲乙两人同时在道路的A点相背而行,甲的速度比乙快,经过5分钟在D点相遇,两人又经过50分钟应在哪里相遇?
如图,A、B、C、D、E、F、G、H是把圆形道路平均分成的8个点.甲乙两人同时在道路的A点相背而行,甲的速度比乙快,经过5分钟在D点相遇,两人又经过50分钟应在哪里相遇? 分析 设圆形道路的周长为8a,则每等份长为a,由题意可得到甲1分钟走的路程为a,从而可算出又经过50分钟以后甲走的路程,因为一圈8个格,所以甲走了50÷8=6(圈)…2(格),进一步解决问题.
解答 解:设圆形道路的周长为8a,则每等份长为a.
由题意可知:甲5分钟走的路程为5a,即甲1分钟走的路程为a,
所以又经过50分钟以后,甲走的路程为50a.
即甲走了50÷8=6(圈)…2(格),
所以50a=8a×6+2a,
因为第一次在D点相遇,所以又经过50分钟后两人在B点相遇.
答:又经过50分钟以后,两人应在B点相遇.
点评 本题考查的有关圆形道路的问题,运用带余除法是解决本题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:小学数学 来源: 题型:解答题
| $\frac{5}{9}$+$\frac{8}{15}$+$\frac{1}{15}$+$\frac{4}{9}$ | $\frac{5}{12}$+$\frac{7}{8}$+$\frac{7}{12}$ | $\frac{13}{25}$-$\frac{13}{50}$+$\frac{1}{5}$ |
| 7-($\frac{3}{4}$-$\frac{2}{5}$) | $\frac{2}{3}$-$\frac{2}{9}$+$\frac{1}{3}$-$\frac{7}{9}$ | $\frac{3}{4}$-($\frac{1}{2}$+$\frac{1}{4}$) |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
| 年份 | 2000年 | 2001年 | 2002年 | 2003年 | 2004年 | 2005年 |
| 数量/台 | 30 | 32 | 30 | 44 | 53 | 65 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com