练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    规定1！=1×1，2！=2×1，3！=3×2×，…已知a！=5040，那么a=（　　）
    分析：1！=1×1，2！=2×1，3！=3×2×1，…可知：
    a！=a×（a-1）×（a-2）×（a-3）×…×2×1；
    a！=5040，求a就是求1×2×3×4×…×a=5040；逐步计算，看乘到哪个数积是5040即可．
    解答：解：a！=5040，即1×2×3×4×…×a=5040；
    因为1×2×3×4×5×6×7=5040；
    所以a=7；
    故选：C．
    点评：本题理解a！的计算方法，然后由此逐数相乘求解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：

    规定1△3=1×2×3，2△4=2×3×4×5，4△3=4×5×6，则（6△4）÷（4△4）=
    3.6
    3.6
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    规定：如图1中，方格里的数表示在其周围8个方格中共有多少个△．即以“1”为中心，在它的四周8个方格中只能有1个△；以“2”为中心，在它的四周8个方格中只能有2个△；以“3”为中心，在它的四周8个方格中只能有3个△；依此类推．

    按上述规定，在如图2中一共可以画12个△．现在已经画好了其中的2个，请你在合适的空格中补上其余的10个．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    如图，圆周上顺次排列着1、2、3、…、12这十二个数，我们规定：相邻的四个数a1、a2、a3、a4顺序颠倒为a4、a3、a2、a1，称为一次“变换”（如：1、2、3、4变为4、3、2、1，又如：11、12、1、2变为2、1、12、11）．能否经过有限次“变换”，将十二个数的顺序变为9、1、2、3、…8、10、11、12（如图）？请说明理由．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

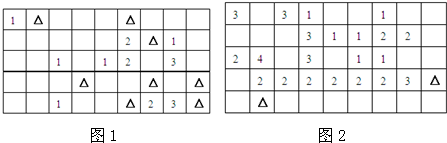
    （1）5678-1999                             （2）8765+1998
    （3）1+2+3+…+99+100                        （4）2+4+6+…+100
    （5）规定a△b=3×a-2×b，①求 3△2，2△3；②求（17△6）△2．

    查看答案和解析>>

    同步练习册答案