Question

【题目】如图， BC=4dm，AC=3dm，CD:AD=1：2，将钝角三角形ABD沿着AD边旋转得到一个封闭图形

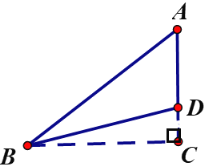
（1）三角形ABD的面积是多少平方分米？

（2）这个封闭图形的体积是多少立方分米？（答案保留整数部分）

Answer 1

【答案】（1）4 ，（2）33

【解析】

（1）CD:AD=1：2，AC=3dm可以求出AD和CD的长度。三角形面积可得解。

（2）根据圆锥的体积公式求解，用三角形ABC形成的圆锥的体积减去三角形BCD形成的圆锥的体积.

（1）CD:AD=1：2，AC=3dm

所以AD=3÷3×2=2（dm）

CD=AC-AD=3-2=1（dm）

三角形ABD的面积是×AD×BC=×2×4=4（）

（2）×π×4×4×3-×π×4×4×1=π≈33（）