在平面中任意作30条直线,这些直线最多可把这个平面分成________部分.
466
分析:一条直线可以把平面分成两部分,两条直线最多可以把平面分成4部分,三条直线最多可以把平面分成7部分,四条直线最多可以把平面分成11部分,可以发现,两条直线时多了2部分,三条直线比原来多了3部分,四条直线时比原来多了4部分,…,n条时比原来多了n部分.
因为n=1,a
1=1+1
n=2,a
2=a
1+2
n=3,a
3=a
2+3
n=4,a
4=a
3+4
…
n=n,a
n=a
n-1+n
以上式子相加整理得,a
n=1+1+2+3+…+n=1+(1+2+3+…+n)=1+

.
解答:一条直线可以把平面分成两部分,
两条直线最多可以把平面分成4部分,
三条直线最多可以把平面分成7部分,
四条直线最多可以把平面分成11部分,
则n条最多可以把平面分成:a
n=1+

.
当n=30时,1+
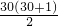
=1+465=466,
答:30条直线最多可把这个平面分成466部分.
故答案为:466.
点评:本题体现了由“特殊到一般再到特殊”的思维过程,有利于培养同学们的探究意识.

 .
. .
.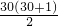 =1+465=466,
=1+465=466,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案