Question

【题目】如图，直角三角形ABC两直角边的长为3、4，M为斜边中点，以两直角边向外作两个正方形．那么三角形MEF的面积是　 　．

Answer 1

【答案】12.25

【解析】

试题分析：我们画图如下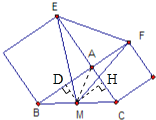连接AM，作MD、MH分别垂直于AB与AC，我们运用△MAE与△MAF及△BAC的面积加在一起就是大△MEF的面积．

解：因为∠EAB=∠FAC=∠BAC=90°，

所以∠EAF=90°，即△EAF是直角三角形，

因为AE=4，AF=3，

所△EAF的面积=3×4÷2=6，

因为M为斜边中点，MD⊥AB，MH⊥AC，

所以MD∥AC且等于AC，MH∥AB且等于，

所以MD==1.5，MH==2，

所以△MAE的面积=4×2=4，△MAF=×3×1.5=2.25，

所以大△MEF的面积=6+4+2.25=12.25；

故答案为：12.25．