Question

小明春游时，看到一农民在田边发愁，原来他想把一块地的面积用直线平均分成两部分，此时农民只带了一把锄头和足够长的细线．小明一看，这是一块梯形的土地，两底分别为AB、CD，于是，小明利用对折细线的方法，找到四条边的中点，并按照如图1所示的方法将土地分成了面积相等的两部分你能否再帮助小明设计出两种不同的方法也将这块土地分成面积相等的两部分呢？

Answer 1

解：设梯形上、下底分别为a、b，高为h．
方案一：如图2，连接梯形上、下底的中点E、F，
则S四边形AFED=S四边形FBCE=；
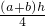
方案二：如图3，连接BD，取BD的中点E，连接AE、EC，
则图中的四边形AECD的面积=梯形ABCD的面积的一半，
因为DE=BE，
所以S△ABE=S△ADE，S△CBE=S△CDE
S△ABE+S△CBE=S△ADE+S△CDE，
四边形AECD的面积=梯形ABCD的面积的一半．
．．
分析：（1）、利用两底的中点，将图形分割成两个梯形，它们的上下底分别相等，高也相等，所以面积也相等；
（2）、连接对角线BD，利用BD的中点E，连接CE和AE，则△ABE的面积=△ADE的面积，△CBE的面积=△CDE的面积，所以AECD和ABCE的面积相等；
点评：本题需仔细分析题意，结合图形，利用中点即可解决问题．
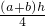