Question

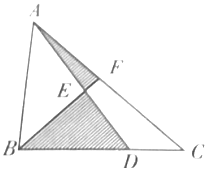
18．AE=ED，BD=2DC，S_△ABC=40cm²，求阴影部分的面积．

Answer 1

分析 连接DF，因为AE=DE，△AEF的面积=△EDF的面积，△ABE的面积=△BDE的面积．因为BD=2DC，所以△BDF的面积=△DCF的面积×2，因此△ABF的面积=△BDF的面积=△DCF的面积×2；所以△ABC的面积=△DCF的面积×5，于是△DCF的面积=40÷5=8（平方厘米）．阴影部分面积等于△BDF的面积=△DCF的面积×2=8×2=16（平方厘米）．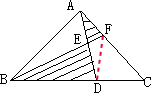

解答 解：连接DF，因为AE=DE，△AEF的面积=△EDF的面积，△ABE的面积=△BDE的面积．
因为BD=2DC，所以△BDF的面积=△DCF的面积×2，因此△ABF的面积=△BDF的面积=△DCF的面积×2；
所以△ABC的面积=△DCF的面积×5；
即S△DCF的面积为：40÷5=8（平方厘米）．
阴影部分面积为：
=△BDF的面积
=△DCF的面积×2
=8×2
=16（平方厘米）
答：阴影部分的面积是16平方厘米．

点评 解答此题的关键是先连接DF，然后根据三角形面积和比的正比关系进行分析，进而得出结论．