练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
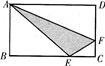
    已知AB=9厘米，AD=12厘米，三角形ABE和三角形ADF的面积各占长方形ABCD的
    13
    ，求三角形AEF的面积．
    分析：先求出长方形的面积，再乘
    1
    3
    ，分别求出三角形ABE和三角形ADF的面积及四边形AECF的面积，再根据三角形的面积公式分别求出BE和DF的长是多少，进而求出三角形CEF的面积，进而可求出三角形AEF的面积．
    解答：解：9×12×
    1
    3
    =36（平方厘米）
    DF=36×2÷12=6（厘米）
    CF=9-6=3（厘米）
    BE=36×2÷9=8（厘米）
    EC=12-8=4（厘米）
    S△CEF=3×4÷2=6（平方厘米）
    S△AEF=36-6=30（平方厘米）
    答：三角形AEF的面积是30平方厘米．
    点评：本题的难点是求出BE、DF的长，进而求出三角形CEF的面积，从而求出三角形AEF的面积是多少．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：

    如图是一种电脑射击游戏的示意图，线段CD、EF和GH的长度都是20厘米，O、P、Q是它们的中点，并且位于同一条直线AB上，AO=45厘米，OP=PQ=20厘米，已知CD上的小圆环的速度是每秒5厘米，EF上的小圆环的速度是每秒9厘米，GH上的小圆环的速度是每秒27厘米．零时刻，CD、EF、GH上各有一个小圆环从左端点同时开始在线段上匀速往返运动．问：此时，从点A向B发射一颗匀速运动的子弹，要想穿过三个圆环，子弹的速度最大为每秒多少厘米？

    查看答案和解析>>

    同步练习册答案