����⣺��1����D��DH��y���ڵ�H����AH=x��

��tanA=
=
=2��
��DH=2x��
��OA=2CD=2OH��
��CD=OH=x��OC=OB=2x��
��S
����AOCD=
��CD+AB��•OC����5=
��x+4x��•2x��
��ã�x=1��
��OC=OB=2x=2��
��OC=OB=2��
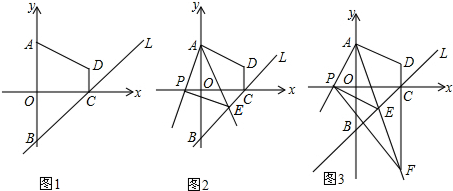
��C�������ǣ�2��0����B�������ǣ�0��2����
��ֱ��l�Ľ���ʽ�ǣ�y=kx+b����
��
��ã�
��
�����Ľ���ʽ�ǣ�y=x-2��
��2����һ�����������P��x�Ḻ����ʱ������AC����OA=OC=OB=2��
���ACB=90�㣬��OAC=45�㣬
���ACE=��AOP=90�㣬
�ߡ�2+��3=45�㣬��1+��3=45�㣬
���1=��2��
���ACE�ס�APO��
��
=
=
����CE=
OP��
����E��EG��x�ᣬ�ڵ�G��
��OC=OB=2��
���OCB=45�㣬
���CEG�ǵ���ֱ�������Σ�
��CE=
EG��
��OP=EG=x��
��S
��PEC=
PC•EG=
��x+2��•x=
x
2+2x��
�ڶ������������P���߶�OC��ʱ��
�ߡ�ACB=90�㣬
���ACE+��AOP=90�㣬
�ߡ�1+��3=90�㣬��2+��3=90�㣬
���1=��2��
���AOP�ס�ACE��
��
=
=
��
��CE=
OP��
��E��EG��x�ᣬ��ֱ��G���ɵõ�����CEG��

��CE=
EG��
��EG=OP=x��
S
��PEC=
PC•EG=
��2-x��•x=
x
2+x��
���������������P���߶�OC��ʱ
ͬ���ɵã���AOP�ס�ACE��
��
=
=
��
��CE=
OP��
��E��x��Ĵ��ߣ�������G���ɵõ���ֱ�ǡ�CEG��
��CE=
EG��
��EG=OP=x��

��S
��PEC=
PC•EG=
��x-2��•x=
x
2-2x��
�൱P��x�Ḻ�����ϣ�S=
x
2+2x��
��P���߶�OC��ʱ��S=-
x2+x��
��P��OC�ӳ�����ʱ��S=
x
2-2x��
��3����һ���������S=
����s=
x
2+2x����ã�x
1=1��x
2=-3������ȥ����
��OP=EG=1����E��a��-1����
���y=-1����y�Tx-2�ã�a=1����E��1��-1����
��A�������ǣ�0��2����
��ֱ��AE�Ľ���ʽ��y=-3x+2��
��A��0��2����
��ֱ��AE�Ľ���ʽ�ǣ�y=-3x+2��
��OC=2����F��2��b������y=-3x+2����b=-4��
��F��2��-4����
ֱ�ǡ�PCF�У�PC=3��CF=4����PF=5��
��E��EN��PF��������N����
��3��4=
��3��1+
��4��1+
��5•EN��
��ã�EN=1��
��EG��PC��EN��PF��EG=EN=1��
���PFE=��EPC��
�ٵ���PEM=��PEFʱ����PEM�ա�PEF����ʱPM=PF=5��

��M
1��4��0����
����PME=��PEFʱ����PEM
2�ס�PEM
1��
��PE
2=PM
2•PM
1��2
2+1
2=PM
2��5��
��PM
2=1��
��O��M
2�غϣ�
��M
2��0��0����
�ڶ��������
��S=
����S=-
x
2+x�У�x
2-2x+3=0������0�������⣻
�����������
��S=
����S=
x
2-2x�У���ã�x
1=-1����ȥ����x
2=3��
��EG=OP=3����E��a��3������y=x-2�ã�a=5��
��E�������ǣ�5��3����
��A��0��2����
��ֱ��AE�Ľ���ʽ�ǣ�y=
x+2��
��OC=2����F�������ǣ�2��b��������y=
x+2���ã�b=
��
��ֱ�ǡ�CPF�У���CP=1��CF=
��

��PF=
��
��E��EN��PE�������������S
��CEF+S
��CPE-S
��PEF=S
��PCF��
��
CF•NC+
PF•EN=
CP•EF����
��3+1��3-
EN=1��
��
��EN=3��
��EN��PF��EN��PN��EN-EG=3��
���FPE=��EPN��
�ٵ���EM
3P=��EFPʱ����EPM
3�ա�EFP����ʱPM
3=PF=
��
��OM
3=
+3=
��
��M
3��
��0����
�ڵ���PEM
4=��EFPʱ����EPM
4�ס�M
3PE����PE
2=PM
3•PM
4��
����
��
2=
PM
4��
��PM
4=5��
��M
4�������ǣ�8��0����
��֮����P��x��ĸ�����ʱ��M�������ǣ�4��0����0��0������P���߶�OC��ʱ�������ڣ���P��OC��ʱ��M�������ǣ�
��0����8��0����









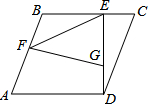 ƽ���ı���ABCD�У�DE��BC��E����DE=BC��EG=BE����G��GF��AB��F������EF��
ƽ���ı���ABCD�У�DE��BC��E����DE=BC��EG=BE����G��GF��AB��F������EF��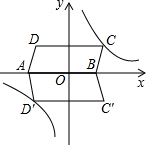 ƽ���ı���ABCD��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ������A��-6��0����B��4��0����C��5��3��������������y=
ƽ���ı���ABCD��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ������A��-6��0����B��4��0����C��5��3��������������y=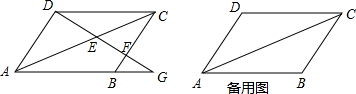
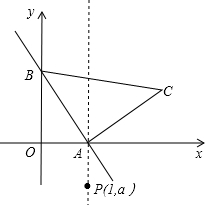 ��֪��ֱ��y=-
��֪��ֱ��y=-