
分析 (1)根据一次函数的性质得1-2k>0,然后解不等式;
(2)根据一次函数与系数的关系得到2k+1>0,然后解不等式即可;
(3)根据一次函数与系数的关系得到2k+1=0,然后解方程即可;
(4)根据一次函数与系数的关系得到1-2k<0且2k+1>0,然后求出两不等式的公共部分即可;
(5)根据一次函数与系数的关系得到1-2k>0且2k+1≥0,然后求出两不等式的公共部分即可.
解答 解:(1)当1-2k>0时,y随x的增大而增大,即k<$\frac{1}{2}$;
(2)当2k+1>0时,函数图象与y轴的交点在y轴的正半轴,即k>-$\frac{1}{2}$;
(3)当2k+1=0时,函数图象经过坐标系原点,即k=-$\frac{1}{2}$;
(4)当1-2k<0且2k+1>0时,函数图象经过第一、二、四象限,所以k>$\frac{1}{2}$;
(5)当1-2k>0且2k+1≥0时,函数图象不经过第四象限,所以-$\frac{1}{2}$≤k<$\frac{1}{2}$.
点评 本题考查了一次函数与系数的关系:由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.当k>0,b>0?y=kx+b的图象在一、二、三象限;k>0,b<0?y=kx+b的图象在一、三、四象限;k<0,b>0?y=kx+b的图象在一、二、四象限;k<0,b<0?y=kx+b的图象在二、三、四象限.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
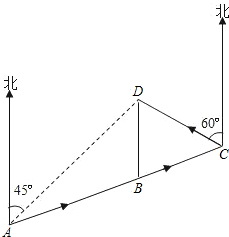 为解决郑州交通拥堵的问题,政府决定北在A、D两地修建高架路,为此,公交车不得不更改线路,原来直接由A到D的公交车现改为由A-B-C-D,如图,其中A、B、C三地在同一直线上,D地在A地北偏东45°方向,在B地正北方向,在C地北偏西60°方向.C地在A地北偏东75°方向,B、D两地相距2km.问更改线路后公交车多行了多远?(结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
为解决郑州交通拥堵的问题,政府决定北在A、D两地修建高架路,为此,公交车不得不更改线路,原来直接由A到D的公交车现改为由A-B-C-D,如图,其中A、B、C三地在同一直线上,D地在A地北偏东45°方向,在B地正北方向,在C地北偏西60°方向.C地在A地北偏东75°方向,B、D两地相距2km.问更改线路后公交车多行了多远?(结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,E、F分别在BC、AD上,且AF=CE,连接EF,与对角线BD交于点O.若EF、BD互相平分,试判断四边形ABCD的形状,并说明理由.
如图,在四边形ABCD中,E、F分别在BC、AD上,且AF=CE,连接EF,与对角线BD交于点O.若EF、BD互相平分,试判断四边形ABCD的形状,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com