
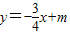 与x轴y轴分别交于点A和点B,点B的坐标为(0,6)
与x轴y轴分别交于点A和点B,点B的坐标为(0,6)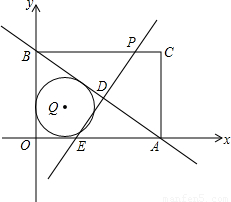
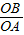 •OB=
•OB= ×6=
×6= ,进而利用当0<t≤
,进而利用当0<t≤ 时,当
时,当 <t≤8时,当8<t≤14时分别得出即可;
<t≤8时,当8<t≤14时分别得出即可; 解:(1)把(0,6)代入
解:(1)把(0,6)代入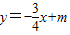
 x+6,
x+6, x+6=0,
x+6=0, =
=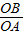 ,
,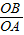 •OB=
•OB= ×6=
×6= ,
, 时,BP=t,则BE=
时,BP=t,则BE= t=
t= t,
t, t•
t• t=48-
t=48- t2;
t2; <t≤8时,BP=t,PC=8-t,
<t≤8时,BP=t,PC=8-t, ,
, )=
)= -t,
-t, [(8-t)+(
[(8-t)+( -t)]•6=
-t)]•6= -t;
-t; (14-t),
(14-t), ×
× (14-t)2=
(14-t)2= (14-t)2;
(14-t)2;
 (6+8+10)r=
(6+8+10)r= ×6×8,
×6×8, IJ=1.2,
IJ=1.2,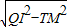 =1.6,
=1.6,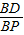 =
= ,
, BD=7,
BD=7, x+6与P′E′垂直,
x+6与P′E′垂直,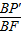 =
= ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| c2 |
| 4 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
(本小题满分11分)已知直线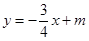 与
与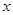 轴
轴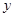 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)
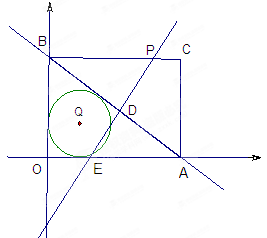
(1)求的![]() 值和点A的坐标;
值和点A的坐标;
(2)在矩形OACB中,点P是线段BC上的一动点,直线PD⊥AB于点D,与![]() 轴交于点E,设BP=
轴交于点E,设BP=![]() ,梯形PEAC的面积为
,梯形PEAC的面积为![]() 。
。
①求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
②⊙Q是△OAB的内切圆,求当PE与⊙Q相交的弦长为2.4时点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
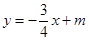 与
与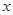 轴
轴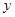 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)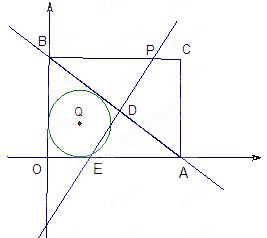
 值和点A的坐标;
值和点A的坐标; 轴交于点E,设BP=
轴交于点E,设BP= ,梯形PEAC的面积为
,梯形PEAC的面积为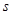 。
。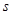 与
与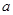 的函数关系式,并写出
的函数关系式,并写出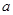 的取值范围;
的取值范围;查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(四川内江卷)数学 题型:解答题
(满分8分)如图,已知直线AB与 轴交于点C,与双曲线
轴交于点C,与双曲线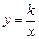 交于A(3,
交于A(3,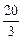 )、B(-5,
)、B(-5,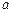 )两点.AD⊥
)两点.AD⊥ 轴于点D,BE∥
轴于点D,BE∥ 轴且与
轴且与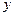 轴交于点E.
轴交于点E.
(1)求点B的坐标及直线AB的解析式;
(2)判断四边形CBED的形状,并说明理由.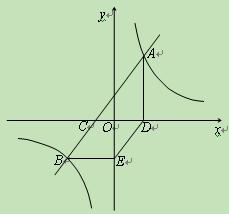
查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北武汉部分学校九年级5月供题调研数学试卷(解析版) 题型:解答题
如图1,已知抛物线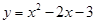 与x轴交于点A和点B,与y轴相交于点C.
与x轴交于点A和点B,与y轴相交于点C.
1.求A、B、C三点的坐标
2.点D为射线CB上的一动点(点D、B不重合),过点B作x轴的垂线BE与以点D为顶点的抛物线y=(x-t)2+h相交于点E,从△ADE和△ADB中任选一个三角形,求出当其面积等于△ABE的面积时的t的值;(友情提示:1、只选取一个三角形求解即可;2、若对两个三角形都作了解答,只按第一个解答给分.)
3.如图2,若点P是直线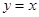 上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
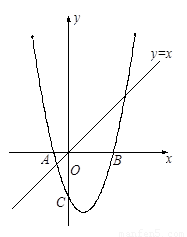
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com