
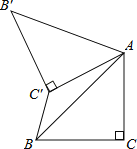
【题目】如图,已知△ABC中,∠C=90°,AC=BC,将△ABC绕点A顺时针方向旋转60°到△AB'C'的位置,连接C′B,C′B=![]() ﹣1,则AC=_____.
﹣1,则AC=_____.
【答案】![]() .
.
【解析】
如图,连接BB′,延长BC'交AB'于点H,由旋转的性质可得AB=AB′,∠BAB′=60°,可证△ABB′为等边三角形,由“SSS”可证△BB′C′≌△BAC,可得∠B′BC′=∠ABC′=30°,由等边三角形的性质和直角三角形的性质可求解.
解:如图,连接BB′,延长BC'交AB'于点H,
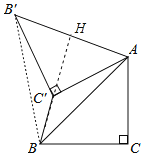
∵将△ABC绕点A顺时针方向旋转60°到△AB'C'的位置,
∴AB=AB′,∠BAB′=60°,
∴△ABB′为等边三角形,
∴∠B′BA=60°,BB′=BA;
在△BB′C′与△BAC中,
 ,
,
∴△BB′C′≌△BAC(SSS),
∴∠B′BC′=∠ABC′=30°,且AB=BB',
∴BH⊥AB',AH=B'H,
∴BH=![]() AH,
AH,
∵AC'=B'C',∠AC'B'=90°,C'H⊥AB'
∴AH=C'H,
∵BC'=BH﹣C'H=![]() AH﹣AH=
AH﹣AH=![]() ﹣1,
﹣1,
∴AH=1,
∴AB'=2=AB,
∵∠C=90°,AC=BC,
∴AB=![]() AC,
AC,
∴AC=![]() ,
,
故答案为![]()


科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.

(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2,为什么?
(3)怎样围才能使围出的矩形场地面积最大?最大面积为多少?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级某班学生准备去购买《英汉词典》一书,此书的标价为20元.现A、B两书店都有此书出售,A店按如下方法促销:若只购买1本,则按标价销售;当一次性购买多于1本,但不多于20本时,每多购买一本,每本的售价在标价的基础上优惠2%(例如,买2本每本的售价优惠2%,买3本每本的售价优惠4%,依此类推);当购买多于20本时,每本的售价为12元.B书店一律按标价的7折销售.
(1)试分别写出在两书店购买此书的总价yA、yB与购书本数之间的函数关系式.
(2)若该班一次购买多于20本,去哪家书店购买更合算?为什么?若要一次性购买不多于20本,先写出y(y=yA﹣yB)与购书本数x之间的函数关系式,画出其函数图象,再利用函数图象分析去哪家书店购买更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面院墙,用篱笆围成一个外形为矩形的花圃,花圃的面积为S平方米,平行于院墙的一边长为x米.
(1)若院墙可利用最大长度为10米,篱笆长为24米,花圃中间用一道篱笆间隔成两个小矩形,求S与x之间的函数关系;
(2)在(1)的条件下,若围成的花圃面积为45平方米,求AB的长;
(3)在(1)的条件下,能否围成面积比45平方米更大的花圃?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中的点Q,我们记点Q到横轴的距离为d1,到纵轴的距离为d2,规定:若d1≥d2,则称d1为点Q的“系长距”;若d1<d2,则称d2为点Q的“系长距”
例如:点Q(3,﹣4)到横轴的距离d1=4,到纵轴的距离d2=3,因为4>3,所以点Q的系长距”为4
(1)①点A(﹣6,2)的“系长距”为 ;②若点B(a,2)的“系长距”为4,则a的值为 .
(2)已知A(3,0),B(0,4),点P为线段AB上的一点,且PB:PA=2:3,点P的“系长距”.
(3)若点C在双曲线y=![]() 上,且点C的“系长距”为6,求点C的坐标.
上,且点C的“系长距”为6,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.
求证:BE+CF=![]() AB.
AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-x2+2x+3.
(1)求函数图像的顶点坐标,并画出这个函数的图像;
(2)根据图像,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当-2<x<2时,函数值y的取值范围;
③若经过点(0,k)且与x轴平行的直线l与y=-x2+2x+3的图像有公共点,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,E是正方形ABCD边AB上的一点,连接BD、DE,将∠BDE绕点D逆时针旋转90°,旋转后角的两边分别与射线BC交于点F和点G.

①线段DB和DG的数量关系是 ;
②写出线段BE,BF和DB之间的数量关系.
(2)当四边形ABCD为菱形,∠ADC=60°,点E是菱形ABCD边AB所在直线上的一点,连接BD、DE,将∠BDE绕点D逆时针旋转120°,旋转后角的两边分别与射线BC交于点F和点G.
①如图2,点E在线段AB上时,请探究线段BE、BF和BD之间的数量关系,写出结论并给出证明;
②如图3,点E在线段AB的延长线上时,DE交射线BC于点M,若BE=1,AB=2,直接写出线段GM的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com