【题目】已知二次函数y＝－x2＋2x＋3．
(1)求函数图像的顶点坐标，并画出这个函数的图像；
(2)根据图像，直接写出：
①当函数值y为正数时，自变量x的取值范围；
②当－2＜x＜2时，函数值y的取值范围；
③若经过点（0，k）且与x轴平行的直线l与y＝－x2＋2x＋3的图像有公共点，求k的取值范围．
【答案】(1)y＝－(x－1)2＋4,顶点（1，4）;（2）①－1＜x＜3,②－5＜y≤4, ③ k≤4 .
【解析】
（1）根据二次函数y＝－x2＋2x＋3求出顶点坐标，利用描点法画出函数图象（2）根据函数图象直接写出结果.
（1）二次函数y＝－x2＋2x＋3的两个解为：x=-1，x=3，顶点坐标为（1,4），由于x2的系数为负数，则函数开口向下．由此可画图得：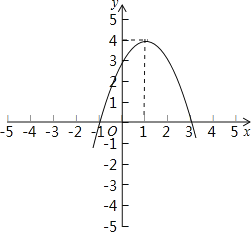
（2）①根据图象可知，当函数值y为正数时，自变量x的取值范围为-1＜x＜3
②当－2＜x＜2时，函数值y的取值范围为-5＜y＜3
③若经过点（0，k）且与x轴平行的直线l与y＝－x2＋2x＋3的图像有公共点， k的取值范围为k≤4
科目：初中数学 来源： 题型：
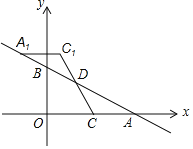
【题目】如图，一次函数y=-
x+m（m＞0）的图象与x轴、y轴分别交于点A、B，点C在线段OA上，点C的横坐标为n，点D在线段AB上，且AD=2BD，将△ACD绕点D旋转180°后得到△A1C1D.
（1）若点C1恰好落在y轴上，试求
的值；
（2）当n=4时，若△A1C1D被y轴分得两部分图形的面积比为3：5，求该一次函数的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，反比例函数y= 
的图象与一次函数y=x+b的图象交
于点A（1，4）、点B（-4，n）．
（1）求一次函数和反比例函数的解析式；
（2）求△OAB的面积；
（3）直接写出一次函数值大于反比例函数值的自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为弘扬中华传统文化，某校举办了学生“国学经典大赛”．比赛项目为：
．唐诗；
．宋词；
．论语；
．三字经．比赛形式分“单人组”和“双人组”．
（1）小丽参加“单人组”，她从中随机抽取一个比赛项目，恰好抽中“三字经”的概率是多少？
（2）小红和小明组成一个小组参加“双人组”比赛，比赛规则是：同一小组的两名队员的比赛项目不能相同，且每人只能随机抽取一次，则小红和小明都没有抽到“论语”的概率是多少？请用画树状图或列表的方法进行说明．
查看答案和解析>>
科目：初中数学 来源： 题型：
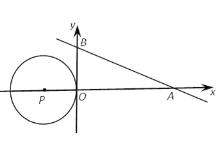
【题目】如图，直线y＝－
x＋2
与x轴、y轴分别相交于A、B两点，圆心P的坐标为（－2，0），⊙P与y轴相切于点O．若将⊙P沿x轴向右移动，当⊙P与该直线相交时，满足横坐标为整数的点P的个数是（ ）
A. 3 B. 4 C. 5 D. 7
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，抛物线G：y=ax2-4ax+3a-2（a≠0），其顶点为C，直线l：y=ax-2a+1（a≠0）与x轴、y轴分别交于A，B两点．
（1）当抛物线G的顶点C在x轴上时，求a的值；
（2）当a＞0时，若△ABC的面积为2，求a的值；
（3）若点Q（m，n）在抛物线G上，把抛物线G绕着点P（t，-2）旋转180°，在1≤m≤3时，总有n随着m的增大而增大，请直接写出t的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中有一直角三角形AOB，O为坐标原点，OA＝1，tan∠BAO＝3，将此三角形绕原点O逆时针旋转90°，得到△DOC，抛物线y＝ax2+bx+c经过点A、B、C．
(1)求抛物线的解析式；
(2)若点P是第二象限内抛物线上的动点，其横坐标为t，设抛物线对称轴l与x轴交于一点E，连接PE，交CD于F，求以C、E、F为顶点三角形与△COD相似时点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】等腰直角三角形 ABC 中，BAC 90° ，AB AC 6 
，D，E 是线段 BC 上的动点，且 DAE 45°
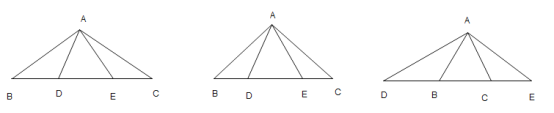
（1）如图 1，请直接写出 BD，DE，EC 满足的关系式为 ，
（2）①如图 1， CE 3 ，请求出 ADE 的面积（写出过程）；
②如图 2， EAC 30° ，请求出 CE 的长度（写出过程）；
（3） 如图 3，D，E 运动到了线段的延长线上，且满足 DAE 135°，CE=8，直接写出 BD的长为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
