腰长为13cm,底长为1Ocm的等腰三角形,若以底边中点为圆心,6cm长为半径作圆,则顶角的顶点在( )
A.圆上
B.圆内
C.圆外
D.无法确定
【答案】
分析:在等腰三角形的腰和底边高线所构成的直角三角形中,根据勾股定理即可求得底边上高线的长度,再根据底边中点到顶点的距离即可判断出顶角的顶点在什么位置.
解答: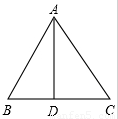
解:如图:
AB=AC=13cm,BC=10cm.
△ABC中,AB=AC,AD⊥BC;
∴BD=DC=

BC=5cm;
Rt△ABD中,AB=13cm,BD=5cm;
由勾股定理,得:AD=
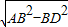
=12cm.
所以底边中点到顶点的距离为12cm,因此顶角的顶点一定在圆的外部.
故选C.
点评:此题考查了点与圆的位置关系,根据等腰三角形的性质以及勾股定理的应用得出底边中点到顶点的距离是解题的关键.
