
 ,坝高为5 m,坝顶CD =" 6" m,现有一工程车需从距B点50 m的A处前方取土,然后经过B—C—D放土,为了安全起见,工程车轮只能停在离A、D处1 m的地方即M、N处工作,已知车轮半经为1 m,求车轮从取土处到放土处圆心从M到N所经过的路径长。(tan150=2-
,坝高为5 m,坝顶CD =" 6" m,现有一工程车需从距B点50 m的A处前方取土,然后经过B—C—D放土,为了安全起见,工程车轮只能停在离A、D处1 m的地方即M、N处工作,已知车轮半经为1 m,求车轮从取土处到放土处圆心从M到N所经过的路径长。(tan150=2- )
)
|




 ,则BL=BR=2-
,则BL=BR=2-
 )=48+
)=48+ m,BC=2×5=10m,
m,BC=2×5=10m, )=8+
)=8+ m;
m; =
=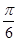 m;圆心从I到N移动的距离是:6-1="5" m,
m;圆心从I到N移动的距离是:6-1="5" m, )+(8+
)+(8+ )+5+
)+5+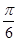 =60+2
=60+2 +
+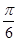 (m).
(m).

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ),点O是这段弧的圆心,C是
),点O是这段弧的圆心,C是 上一点,OC⊥AB,垂足为D,AB=300m,CD=50m,则这段弯路的半径是 m.
上一点,OC⊥AB,垂足为D,AB=300m,CD=50m,则这段弯路的半径是 m.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 ,求BF的长.
,求BF的长.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com