
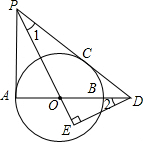
 如图,AB是⊙O的直径,PA,PC分别与⊙O相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E,记∠EPD=∠1,∠EDO=∠2.
如图,AB是⊙O的直径,PA,PC分别与⊙O相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E,记∠EPD=∠1,∠EDO=∠2.分析 (1)根据切线长定理和切线的性质即可证明:∠1=∠2;
(2)连接OC,利用tan∠PDA=$\frac{3}{4}$,可求出CD=4,再证明△OED∽△DEP,根据相似三角形的性质和勾股定理即可求出OE的长.
解答 证明:∵PA,PC与⊙O分别相切于点A,C,
∴∠APO=∠1且PA⊥AO,
∴∠PAO=90°,
∵∠AOP=∠EOD,∠PAO=∠E=90°,
∴∠APO=∠2,
∴∠1=∠2;
(2)解:连接OC,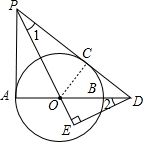
∴PA=PC=6,
∵tan∠PDA=$\frac{3}{4}$,
∴在Rt△PAD中,AD=8,PD=10,
∴CD=4
∵tan∠PDA=$\frac{3}{4}$,
∴在Rt△OCD中,OC=OA=3,OD=5,
∵∠EPD=∠ODE,
∴△OED∽△DEP,
∴$\frac{PD}{DO}$=$\frac{PE}{DE}$=$\frac{ED}{OE}$=2,
∴DE=2OE
在Rt△OED中,OE2+DE2=OD2,即5OE2=52,
∴OE=$\sqrt{5}$.
点评 本题综合考查了切线长定理,相似三角形的性质和判定,勾股定理的应用,能综合运用性质进行推理和计算是解此题的关键,通过做此题培养了学生的分析问题和解决问题的能力.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
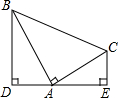 如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的垂线BC、CE,垂足分别为D、E,若BD=3,CE=2,求DE的长.
如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的垂线BC、CE,垂足分别为D、E,若BD=3,CE=2,求DE的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 城市 | 北京 | 上海 | 杭州 | 苏州 | 武汉 | 重庆 | 广州 | 福州 | 南宁 | 深圳 |
| 最高温度(℃) | 21 | 25 | 28 | 27 | 26 | 31 | 29 | 28 | 30 | 29 |
| A. | 27 | B. | 28 | C. | 29 | D. | 31 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7环 | B. | 8环 | C. | 9环 | D. | 10环 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
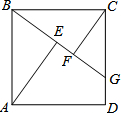 如图,在正方形ABCD中,点G是CD上任意一点,连接BG,作AE⊥BG于点E,CF⊥BG于点F.
如图,在正方形ABCD中,点G是CD上任意一点,连接BG,作AE⊥BG于点E,CF⊥BG于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 荔枝 品 种 | A | B | C |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
| 每吨荔枝获得(百元) | 12 | 16 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com