练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在正方形ABCD中，E、F分别是AB、BC上的点，且AE=BF．求证：CE=DF．

     

     

    证明见解析.

    【解析】

    试题分析：根据正方形的性质可得AB=BC=CD，∠B=∠BCD=90°，然后求出BE=CF，再利用“边角边”证明△BCE和△CDF全等，根据全等三角形对应边相等证明即可．

    试题解析：证明：在正方形ABCD中，AB=BC=CD，∠B=∠BCD=90°，

    ∵AE=BF，∴AB﹣AE=BC﹣BF，即BE=CF.

    在△BCE和△CDF中，∵，

    ∴△BCE≌△CDF（SAS）.∴CE=DF．

    考点：1.正方形的性质；2.全等三角形的判定和性质．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014年初中毕业升学考试（广东卷）数学（解析版） 题型：选择题

    如图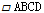，中，下列说法一定正确的是（ ）

    A、AC=BD B、AC⊥BD C、AB=CD D、AB=BC

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（广东深圳卷）数学（解析版） 题型：选择题

    下列方程没有实数根的是（ ）

    A． B．

    C． D．

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（浙江嘉兴卷）数学（解析版） 题型：选择题

    如图，⊙O的直径CD垂直弦AB于点E，且CE=2，DE=8，则AB的长为（ ）

    A．2 B．4 C．6 D．8

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（广西钦州卷）数学（解析版） 题型：解答题

    如图，点B、C、D都在半径为6的⊙O上，过点C作AC∥BD交OB的延长线于点A，

    连接CD，已知∠CDB=∠OBD=30°．

    （1）求证：AC是⊙O的切线；

    （2）求弦BD的长；

    （3）求图中阴影部分的面积．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（浙江嘉兴卷）数学（解析版） 题型：选择题

    如图，在一张矩形纸片ABCD中，AD＝4cm，点E，F分别是CD和AB的中点．现将这张纸片折叠，使点B落在EF上的点G处，折痕为AH．若HG的延长线恰好经过点D，则CD的长为（ ）

    A．2cm B．cm C．4cm D．cm

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（浙江绍兴卷）数学（解析版） 题型：选择题

    计算的结果是（ ）

    A． B． C． D．

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（浙江绍兴卷）数学（解析版） 题型：解答题

    课本中有一道作业题：

    有一块三角形余料ABC，它的边BC=120mm，高AD=80mm．要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上．问加工成的正方形零件的边长是多少mm？

    小颖解得此题的答案为48mm，小颖善于反思，她又提出了如下的问题．

    （1）如果原题中要加工的零件是一个矩形，且此矩形是由两个并排放置的正方形所组成，如图1，此时，这个矩形零件的两条边长又分别为多少mm？请你计算．

    （2）如果原题中所要加工的零件只是一个矩形，如图2，这样，此矩形零件的两条边长就不能确定，但这个矩形面积有最大值，求达到这个最大值时矩形零件的两条边长．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年沪教版初中数学七年级上册第九章9.3整式的乘法练习卷（解析版） 题型：选择题

    [（﹣b）2]3的计算结果为（　　）

    A．﹣b5 B．b5 C．﹣b6 D．b6

     

     

    查看答案和解析>>

    同步练习册答案