
【题目】如图,正方形![]() 中,延长
中,延长![]() 至
至![]() 使
使![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() ,
,![]() 交于点
交于点![]() .则下列说法:①
.则下列说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A.4个B.3个C.2个D.1个
【答案】A
【解析】
根据正方形的性质,以及中点的性质可得△FGN≌△HAN,即证①;利用角度之间的等量关系的转换可以判断②;根据△AKH∽△MKF,进而利用相似三角形的性质即可判断③;设AN=![]() AG=x,则AH=2x,FM=6x,根据△AKH∽△MKF得出
AG=x,则AH=2x,FM=6x,根据△AKH∽△MKF得出![]() ,再利用三角形的面积公式求出△AFN的面积,再利用
,再利用三角形的面积公式求出△AFN的面积,再利用![]() 即可求出四边形DHKM的面积,作比即可判断④.
即可求出四边形DHKM的面积,作比即可判断④.
∵四边形EFGB是正方形,CE=2EB,四边形ABCD是正方形
∴G为AB中点,∠FGN=∠HAN=90°,AD=AB
即FG=AG=GB=![]() AB
AB
又H是AD的中点
AH=![]() AD
AD
∴FG=HA
又∠FNG=∠HNA
∴△FGN≌△HAN,故①正确;
∵∠DAM+∠GAM=90°
又∠NFG+∠FNG=90°
即∠FNG=∠GAM
∵∠FNG+∠NFG+90°=180°
∠AMD+∠DAM+90°=180°
∠FNG=∠GAM=∠AMD
∴![]() ,故②正确;
,故②正确;
由图可得:MF=FG+MG=3EB
△AKH∽△MKF
∴![]()
∴KF=3KH
又∵NH=NF
且FH=KF+KH=4KH=NH+NF
∴NH=NF=2KH
∴KH=KN
∴FN=2NK,故③正确;
∵AN=GN且AN+GN=AG
∴可设AN=![]() AG=x,则AH=2x,FM=6x
AG=x,则AH=2x,FM=6x
由题意可得:△AKH∽△MKF且相似比为:![]()
∴△AKH以AH为底边的高为:![]()
∴![]()
![]()
![]()
∴![]() ,故④正确;
,故④正确;
故答案选择A.


科目:初中数学 来源: 题型:
【题目】(本题9分)把代数式通过配凑等手段,得到完全平方式,再运用完全平方式是非负性这一性质增加问题的条件,这种解题方法叫做配方法.配方法在代数式求值,解方程,最值问题等都有着广泛的应用.
例如:①用配方法因式分解:a2+6a+8
原式=a2+6a+9-1
=(a+3)2 –1
=(a+3-1)(a+3+1)
=(a+2)(a+4)
②若M=a2-2ab+2b2-2b+2,利用配方法求M的最小值:
a2-2ab+2b2-2b+2=a2-2ab+b2+b2-2b+1+1
=(a-b)2+(b-1)2 +1
∵(a-b)2≥0,(b-1)2 ≥0
∴当a=b=1时,M有最小值1
请根据上述材料解决下列问题:
(1)在横线上添上一个常数项使之成为完全平方式:a 2+4a+ .
(2)用配方法因式分解: a2-24a+143
(3)若M=![]() a2+2a +1,求M的最小值.
a2+2a +1,求M的最小值.
(4)已知a2+b2+c2-ab-3b-4c+7=0,求a+b+c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(0,a),B(0,b),C(m,b)且(a-4)2+![]() =0,
=0,![]()
(1)求C点坐标
(2)作DE DC,交y轴于E点,EF为 AED的平分线,且DFE= 90o。 求证:FD平分ADO;
(3)E 在 y 轴负半轴上运动时,连 EC,点 P 为 AC 延长线上一点,EM 平分∠AEC,且 PM⊥EM,PN⊥x 轴于 N 点,PQ 平分∠APN,交 x 轴于 Q 点,则 E 在运动过程中,![]() 的大小是否发生变化,若不变,求出其值.
的大小是否发生变化,若不变,求出其值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把二元一次方程![]() 的一个解用一个点表示出来,例如:可以把它的其中一个解
的一个解用一个点表示出来,例如:可以把它的其中一个解![]() 用点(2,1 )在平面直角坐标系中表示出来
用点(2,1 )在平面直角坐标系中表示出来
探究1:
(1)请你在直角坐标系中标出4个以方程![]() 的解为坐标的点,然后过这些点中的任意两点作直线,你有什么发现,请写出你的发现 .
的解为坐标的点,然后过这些点中的任意两点作直线,你有什么发现,请写出你的发现 .
在这条直线上任取一点,这个点的坐标是方程![]() 的解吗? (填“是”或“不是”___
的解吗? (填“是”或“不是”___
(2)以方程![]() 的解为坐标的点的全体叫做方程
的解为坐标的点的全体叫做方程![]() 的图象.根据上面的探究想一想:方程
的图象.根据上面的探究想一想:方程![]() 的图象是_ _.
的图象是_ _.

探究2:根据上述探究结论,在同-平面直角坐标系中画出二元一次方程组![]() 中的两个二元一次方程的图象,由这两个二元一次方程的图象,请你直接写出二元一次方程组
中的两个二元一次方程的图象,由这两个二元一次方程的图象,请你直接写出二元一次方程组![]() 的解,即
的解,即
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)填空:
①当![]() 的值为_______时,四边形
的值为_______时,四边形![]() 是矩形;
是矩形;
②当![]() 的值为______时,四边形
的值为______时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
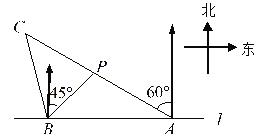
【题目】如图,在一笔直的海岸线![]() 上有
上有![]() 、
、![]() 两个观测站,
两个观测站,![]() 在
在![]() 的正东方向,
的正东方向,![]() (单位:
(单位:![]() )有一艘小船在点
)有一艘小船在点![]() 处,从
处,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,从
的方向,从![]() 测得小船在北偏东
测得小船在北偏东![]() 的方向.(结果保留根号)
的方向.(结果保留根号)
(1)求点![]() 到海岸线
到海岸线![]() 的距离;
的距离;
(2)小船从点![]() 处沿射线
处沿射线![]() 的方向航行一段时间后,到达点
的方向航行一段时间后,到达点![]() 处,此时,从
处,此时,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,求点
的方向,求点![]() 与点
与点![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com