
 如图,AB是半圆的直径,点D是
如图,AB是半圆的直径,点D是 |
| AC |
| A、100° | B、105° |
| C、110° | D、115° |
 |
| AC |
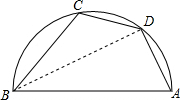 解:连接BD,
解:连接BD, |
| AC |
 |
| CD |
 |
| AD |
| 1 |
| 2 |
| 1 |
| 2 |


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
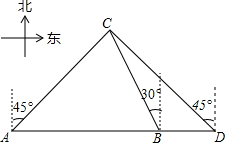 某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时40海里.求A、D两点间的距离.(结果不取近似值)
某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时40海里.求A、D两点间的距离.(结果不取近似值)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,圆A、圆B的半径分别为4、2,且AB=12.若作一圆C使得三圆的圆心在同一直线上,且圆C与另两个圆一个外切、一个内切,则圆C的半径长可能为
如图,圆A、圆B的半径分别为4、2,且AB=12.若作一圆C使得三圆的圆心在同一直线上,且圆C与另两个圆一个外切、一个内切,则圆C的半径长可能为查看答案和解析>>
科目:初中数学 来源: 题型:
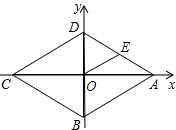 如图,菱形ABCD中,对角线AC、BD相关于点O,且AC=16,BD=12,E为AD的中点,点P在x轴正半轴上移动,若△POE为等腰三角形,则P的坐标是
如图,菱形ABCD中,对角线AC、BD相关于点O,且AC=16,BD=12,E为AD的中点,点P在x轴正半轴上移动,若△POE为等腰三角形,则P的坐标是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com