练习册

  • 练习册
  • 试题
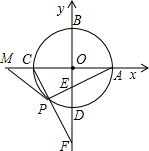    精英家教网 > 初中数学 > 题目详情
    7、如图，已知两条互相垂直的直线a和b相交于点O，试在直线a，b上找一点Q，使得△OPQ为等腰三角形，这样的点Q一共有（　　）
    分析：要求以OP为一边的等腰三角形的情况，分为OP为底，OP为腰（分为∠O或∠P为顶角）几种情况讨论就可以得出结论．
    解答：解：如图，作OP的中垂线与a、b的交点为顶点有2种情况；
    以点P为圆心，OP为半径画弧与a、b的交点有2种情况；
    以点O为圆心，OP为半径画弧与a、b的交点有4种情况．
    ∴共8种情况．

    故选A．
    点评：本题考查的是等腰三角形的判定，实际涉及了等腰三角形的性质，本题可以用作图的方法来解决，要求学生对等腰三角形的性质和判定要很熟悉．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，以⊙O两条互相垂直的直径所在直线为轴建立平面直角坐标系，两坐标轴交⊙O于A，B，C，D四点，点P在弧CD上，连PA交y轴于点E，连CP并延长交y轴于点F．
    （1）求∠FPE的度数；
    （2）求证：OB2=OE•OF；
    （3）若⊙O的半径为
    		3
    ，以线段OE，OF的长为根的一元二次方程为x2-
    5
    2
    		3
    x+m=0，求直线CF的解析式；
    （4）在（3）的条件下，过点P作⊙O的切线PM与x轴交于点M，求△PCM的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：022

    如图，已知⊙O中互相垂直的两条弦AB，CD相交于P，PA＝3，PB＝5，AB的弦心距为3，则CD的弦心距是________，CD＝________，⊙O的半径为________．

    查看答案和解析>>

    科目：初中数学 来源：2000年全国中考数学试题汇编《一次函数》（02）（解析版） 题型：解答题

    （2000•绍兴）如图，以⊙O两条互相垂直的直径所在直线为轴建立平面直角坐标系，两坐标轴交⊙O于A，B，C，D四点，点P在弧CD上，连PA交y轴于点E，连CP并延长交y轴于点F．
    （1）求∠FPE的度数；
    （2）求证：OB2=OE•OF；
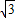    （3）若⊙O的半径为，以线段OE，OF的长为根的一元二次方程为x2-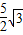x+m=0，求直线CF的解析式；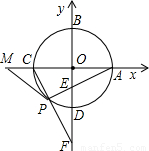
    （4）在（3）的条件下，过点P作⊙O的切线PM与x轴交于点M，求△PCM的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

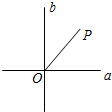    如图，已知两条互相垂直的直线a和b相交于点O，试在直线a，b上找一点Q，使得△OPQ为等腰三角形，这样的点Q一共有


    1. A.
      8个
    2. B.
      7个
    3. C.
      6个
    4. D.
      5个

    查看答案和解析>>

    同步练习册答案