
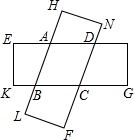
 如图,由两个等宽的矩形叠合而得到四边形ABCD.
如图,由两个等宽的矩形叠合而得到四边形ABCD.分析 (1)作AR⊥BC于R,AS⊥CD于S,根据题意先证出四边形ABCD是平行四边形,再由BC=CD得平行四边形ABCD是菱形;
(2)设BC=x,则CG=6-x,CD=BC=x,在Rt△CDG中,由勾股定理得出x,再求得面积.
解答 解:(1)四边形ABCD是菱形.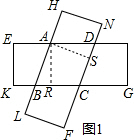
理由:作AR⊥BC于R,AS⊥CD于S,
由题意知:AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∵两个矩形的宽度相等,
∴AR=AS,
∵AR•BC=AS•CD,
∴BC=CD,
∴平行四边形ABCD是菱形;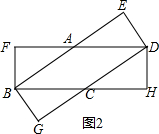
(2)当这两张纸片叠合成如图2时,菱形的面积最大,
设BC=x,则CG=8-x,CD=BC=x,
在Rt△CBG中,CG2+BG2=BC2,
∴(8-x)2+22=x2,
解得x=$\frac{17}{4}$,
∴S=BG•DG=$\frac{17}{2}$.
点评 本题考查了菱形的判定和性质、勾股定理和矩形的性质等知识点,正确的画出图形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
| 人数 | 平均身高(单位:厘米) | 方差 | |
| 男生 | 15 | 175 | 36 |
| 女生 | 15 | 165 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
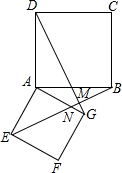 如图,共顶点A的两个正方形ABCD、AEFG,连接DG、BE,且BE交DG于M点,交AG于N点.求证:
如图,共顶点A的两个正方形ABCD、AEFG,连接DG、BE,且BE交DG于M点,交AG于N点.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com