
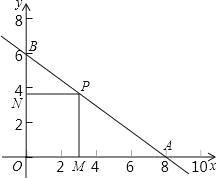
【题目】次函数的图象与x轴、y轴分别交于点A(8,0)和点B(0,6).
(1)确定此一次函数的解析式.
(2)求坐标原点O到直线AB的距离.
(3)点P是线段AB上的一个动点,过点P作PM垂直于x轴于M,作PN垂直于y轴于N,记L=PM+PN,问L是否存在最大值和最小值?若存在,求出此时P点到原点O的距离,若不存在请说明理由.
【答案】(1)、y=﹣![]() x+6;(2)、4.8;(3)、当x=0时,L值最大,最大值为8,此时,点P到原点O的距离为8,x=8时,L值最小,最小值为6,此时,点P到原点O的距离为6.
x+6;(2)、4.8;(3)、当x=0时,L值最大,最大值为8,此时,点P到原点O的距离为8,x=8时,L值最小,最小值为6,此时,点P到原点O的距离为6.
【解析】
试题分析:(1)、设一次函数解析式为y=kx+b,把点A、B的坐标代入函数解析式,利用待定系数法求一次函数解析式解答;(2)、设点O到AB的距离为h,利用勾股定理列式求出AB,再利用△AOB的面积列式计算即可得解;(3)、设AM=x,表示出OM即PN的长,再利用∠BAO的正切值表示出PM,然后列出PM+PN的表达式,再根据一次函数的增减性求解即可.
试题解析:(1)、设一次函数解析式为y=kx+b, ∵函数图象经过点A(8,0)和点B(0,6),
∴![]() , 解得
, 解得 . 所以,函数解析式为y=﹣
. 所以,函数解析式为y=﹣![]() x+6;
x+6;
(2)、设点O到AB的距离为h, ∵点A(8,0)和点B(0,6), ∴OA=8,OB=6,
由勾股定理得,AB=![]() =
=![]() =10, S△AOB=
=10, S△AOB=![]() ×10h=
×10h=![]() ×8×6, 解得h=4.8,
×8×6, 解得h=4.8,
所以,坐标原点O到直线AB的距离为4.8;
(3)、设AM=x, 则OM=OA﹣AM=8﹣x, ∵PM⊥x轴,PN⊥y轴, ∴四边形OMPN是矩形,
∴PN=OM=8﹣x, ∵PM=AMtan∠BAO=![]() x=
x=![]() x, ∴L=PM+PN=
x, ∴L=PM+PN=![]() x+8﹣x=﹣
x+8﹣x=﹣![]() x+8,
x+8,
∵点P是线段AB上的一个动点, ∴点M在线段OA上, ∴0≤x≤8, ∵﹣![]() <0,
<0,
∴当x=0时,L值最大,最大值为8,此时,点P到原点O的距离为8,
x=8时,L值最小,最小值为6,此时,点P到原点O的距离为6.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
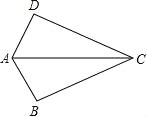
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线![]() 过点A(—1,0),与⊙C相切于点D,
过点A(—1,0),与⊙C相切于点D,
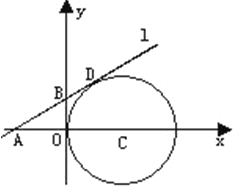
(1)求∠CAD的度数。
(2)求直线![]() 的解析式。
的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016“五一”长假,波月洞景区授待游客约110000人次,将110000用科学记数法表示为( )
A. 11×104 B. 1.1×105 C. 1.1×106 D. 11万
查看答案和解析>>
科目:初中数学 来源: 题型:
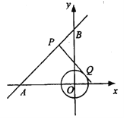
【题目】如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB 上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( ).
A.![]() B.
B.![]() C.2
C.2![]() D.3
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com