
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形. BE交AC于F,AD交CE于H.
(1)求证:△BCE≌△ACD;
(2)试判断△CHF的形状,并说明理由.

【答案】(1)、证明过程见解析;(2)、等边三角形,理由见解析.
【解析】
试题分析:(1)、根据等边三角形的性质得出BC=AC,CE=CD,∠BCA=∠ECD=600 ,从而说明∠BCE=∠ACD,然后得出△BCE和△ACD全等,从而得出答案;(2)、根据全等得出∠CBF=∠CAH,BC=AC,根据三角形共线得出∠FCH=60°,然后证明△BCF和△ACH全等,得出CF=CH,得出等边三角形.
试题解析:(1)、∵![]() 和
和![]() 都是等边三角形 ∴BC=AC,CE=CD,∠BCA=∠ECD=600
都是等边三角形 ∴BC=AC,CE=CD,∠BCA=∠ECD=600
∴∠BCA+∠ACE=∠ECD+∠ACE 即∠BCE=∠ACD ∴△BCE≌△ACD(SAS)
(2)、△CHF等边三角形
由(1)可知△BCE≌△ACD ∴∠CBF=∠CAH,BC=AC.
∵![]() 和
和![]() 都是等边三角形,且点B、C、D在同一条直线上
都是等边三角形,且点B、C、D在同一条直线上
∴∠ACH=180°-∠ACB-∠HCD=600=∠BCF ∴△BCF≌△ACH(ASA)
∴CF=CH ∵∠FCH=600 ∴![]() 等边三角形
等边三角形


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(2y-3z)2 等于( )
A. 4y2-12yz+z2 B. .y2-12yz+9z2 C. 4y2-12yz+9z2 D. .4y2-6yz+9z2
查看答案和解析>>
科目:初中数学 来源: 题型:
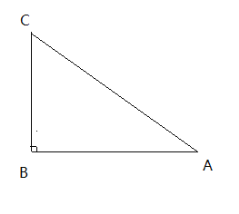
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm。
(1)若P、Q是△ABC边上的两个动点,其中点P从A沿A→B方向运动,速度为每秒1cm,点Q从B沿B→C方向运动,速度为每秒2cm,两点同时出发,设出发时间为t秒.①当t=1秒时,求PQ的长;②从出发几秒钟后,△PQB是等腰三角形?
(2)若M在△ABC边上沿B→A→C方向以每秒3cm的速度运动,则当点M在边CA上运动时,求△BCM成为等腰三角形时M运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行课间操比赛,甲、乙两个班各选出20名学生参加比赛,两个班参赛学生的平均身高都为1.65m,其方差分别是S甲2=3.8,S乙2=3.4,则参赛学生身高比较整齐的班级是( )
A. 甲班B. 乙班C. 同样整齐D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人将1 000元人民币按一年期存入银行,一年后本金和利息共获1 018元,利息已扣除20%利息税,则这种存款的利率是( )
A. 1% B. 2% C. 2.25% D. 10%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com