练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    阅读下列材料：
    ∵
    ∴
    解答问题：
    （1）在式中，第六项为         ，第项为          ，上述求和的想法是通过逆用          法则，将式中各分数转化为两个实数之差，使得除首末两项外的中间各项可以           从而达到求和的目的．
    （2）解方程.
    （1），分式的加减法，相互抵消。
    （2）经检验x=－12和x=2为原方程的解解析:
    本题主要考查分式的加减法
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    阅读下列材料并解答后面的问题：利用完全平方公式（a±b）2=a2±2ab+b2，通过配方可对a2+b2进行适当的变形，如a2+b2=（a+b）2-2ab或a2+b2=（a-b）2+2ab．从而使某些问题得到解决．例：已知a+b=5，ab=3，求a2+b2的值．
    解：a2+b2=（a+b）2-2ab=52-2×3=19．
    问题：（1）已知a+
    1
    a
    =6，则a2+
    1
    a2
    =
     
    ；
    （2）已知a-b=2，ab=3，求a4+b4的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读下列材料：
    为解方程（x2-1）2-5（x2-1）+4=0，我们可以将x2-1看作一个整体，设x2-1=y，则原方程可化为y2-5y+4=0，解得y1=1，y2=4．
    当y1=1时，x2-1=1，∴x=±
    		2
    ；当y2=4时，x2-1=4，∴x=±
    		5
    ．
    因此原方程的解为：x1=
    		2
    ，x2=-
    		2
    ，x3=
    		5
    ，x4=-
    		5
    ．
    （1）已知方程
    1
    x2-2x
    =x2-2x-3    ，如果设x2-2x=y，那么原方程可化为
     
    （写成关于y的一元二次方程的一般形式）．
    （2）根据阅读材料，解方程：x（x+3）（x2+3x+2）=24．

    查看答案和解析>>

    科目：初中数学 来源：学习周报　数学　北师大九年级版　2009－2010学年　第5期　总第161期 北师大版 题型：044

    请阅读下列材料：

    为解方程(x2－1)2－5(x2－1)＋4＝0，我们可以将x2－1视为一个整体，然后设x2－1＝y，则原方程可化为y2－5y＋4＝0，①解得y1＝1，y2＝4．

    当y＝1时，即x2－1＝1，解得x＝±；当y＝4时，即x2－1＝4，解得x＝±．

    所以原方程的解共有四个：x1＝，x2＝－，x3＝，x4＝－．

    请解答下列问题：

    (1)由原方程得到方程①的过程中，运用换元的方法达到了________的目的，这是数学中转化思想的运用；

    (2)运用这种方法解方程：(x2－2x)2－11(x2－2x)＋24＝0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    阅读下列材料：
    为解方程（x2-1）2-5（x2-1）+4=0，我们可以将x2-1看作一个整体，设x2-1=y，则原方程可化为y2-5y+4=0，解得y1=1，y2=4．
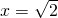    当y1=1时，x2-1=1，∴数学公式；当y2=4时，x2-1=4，∴数学公式．
    因此原方程的解为：数学公式．
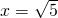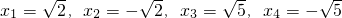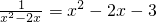    （1）已知方程数学公式，如果设x2-2x=y，那么原方程可化为________（写成关于y的一元二次方程的一般形式）．
    （2）根据阅读材料，解方程：x（x+3）（x2+3x+2）=24．

    查看答案和解析>>

    科目：初中数学 来源：2008年江苏省镇江市丹阳市横塘中学中考数学模拟试卷（解析版） 题型：解答题

    阅读下列材料：
    为解方程（x2-1）2-5（x2-1）+4=0，我们可以将x2-1看作一个整体，设x2-1=y，则原方程可化为y2-5y+4=0，解得y1=1，y2=4．
    当y1=1时，x2-1=1，∴；当y2=4时，x2-1=4，∴．
    因此原方程的解为：．
    （1）已知方程，如果设x2-2x=y，那么原方程可化为______（写成关于y的一元二次方程的一般形式）．
    （2）根据阅读材料，解方程：x（x+3）（x2+3x+2）=24．

    查看答案和解析>>

    同步练习册答案