解:(1)∵抛物线与x轴交于点A(x
1,0)、B(x
2,0),
∴x
1、x
2是关于x的方程x
2-(m+1)x+m=0的解.
解方程,得x=1或x=m.
(1)∵A在B的左侧,m>1,
∴x
1=1,x
2=m.
∴AB=m-1.
抛物线与y轴交于C(0,m)点.
∴OC=m.
△ABC的面积S=
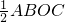
=
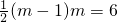
.
解得m
1=4,m
2=-3(不合题意,舍去).
∴抛物线解析式为y=x
2-5x+4;
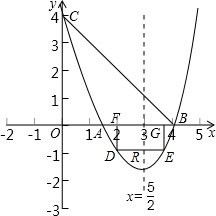
(2)∵点D在(1)中的抛物线上,
∴设D(t,t
2-5t+4)(
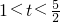
).
∴F(t,0),DF=-t
2+5t-4.
又抛物线对称轴是直线

,DE与抛物线对称轴交点记为R(如图),
∴DR=
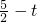
,DE=5-2t.
设矩形DEGF的周长为L,则L=2(DF+DE).
∴L=2(-t
2+5t-4+5-2t)
=-2t
2+6t+2
=
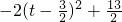
.
∵
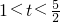
,
∴当且仅当

时,L有最大值.
当

时,L
最大=

.
∴矩形周长的最大值为

.
(3)∵A在B的左侧,m<0,
∴x
1=m,x
2=1.
∴AB=1-m.
如图,作NH⊥AB于H,连接QN.
在Rt△AHN中,
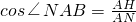
=

.
设AH=4k(k>0),则AN=5k,NH=3k.
∴AP=

=
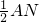
=
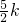
,PH=AH-AP=
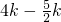
=
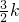
,PN=
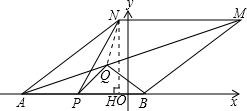
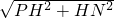
=
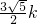
.
∵菱形ABMN是轴对称图形,
∴QN=QB.
∴PQ+QN=PQ+QB=6.
∵PQ+QN≥PN(当且仅当P、Q、N三点共线时,等号成立).
∴6≥
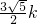
,
解得k≤

.
∵S
菱形ABMN=AB•NH=15k
2≤48.
∴当菱形面积取得最大值48时,k=

.
此时AB=5k=1-m=

.
解得m=1-

.
∴A点的坐标为(1-

,0).
分析:(1)由抛物线y=x
2-(m+1)x+m与x轴交于点A(x
1,0)、B(x
2,0),得出x
2-(m+1)x+m=0的解,再利用m>1,△ABC的面积为6,即△ABC的面积S=
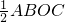
=
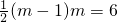
,求出m,从而得出解析式;
(2)作出矩形,用t表示出矩形的周长,利用二次函数的最值求出即可;
(3)首先表示出AB的长度,再利用
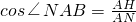
=

,QB+PQ=6,得出S
菱形ABMN=AB•NH=15k
2≤48,当菱形面积取得最大值48时,k=

,由AB=5k=1-m=

.解出m的值,得出A点坐标.
点评:此题主要考查了一元二次方程的解法,以及二次函数的最值问题,锐角三角函数问题和矩形菱形等知识,题目综合性较强.

 角线AM上一点,若
角线AM上一点,若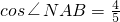 ,QB+PQ=6,当菱形ABMN的面积最大时,求点A的坐标.
,QB+PQ=6,当菱形ABMN的面积最大时,求点A的坐标.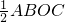 =
=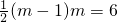 .
.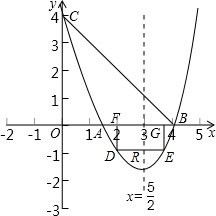
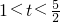 ).
). ,DE与抛物线对称轴交点记为R(如图),
,DE与抛物线对称轴交点记为R(如图),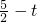 ,DE=5-2t.
,DE=5-2t.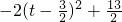 .
.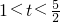 ,
, 时,L有最大值.
时,L有最大值. 时,L最大=
时,L最大= .
. .
.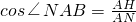 =
= .
. =
=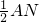 =
=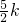 ,PH=AH-AP=
,PH=AH-AP=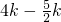 =
=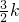 ,PN=
,PN=
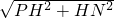 =
=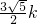 .
.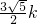 ,
, .
. .
. .
. .
. ,0).
,0).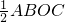 =
=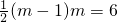 ,求出m,从而得出解析式;
,求出m,从而得出解析式;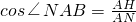 =
= ,QB+PQ=6,得出S菱形ABMN=AB•NH=15k2≤48,当菱形面积取得最大值48时,k=
,QB+PQ=6,得出S菱形ABMN=AB•NH=15k2≤48,当菱形面积取得最大值48时,k= ,由AB=5k=1-m=
,由AB=5k=1-m= .解出m的值,得出A点坐标.
.解出m的值,得出A点坐标.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案