
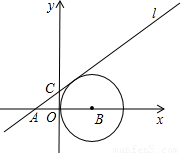
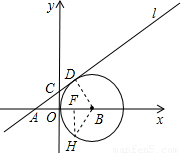
 解:(1)过B作BD垂直l交于点D,
解:(1)过B作BD垂直l交于点D,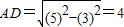 ,
, ,
,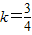 ,
,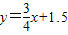 ;
;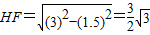 ,
,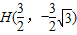 ,
,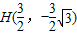 代入y=ax2+bx+c(a>0),
代入y=ax2+bx+c(a>0), ;
;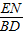 =
=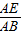 ,即
,即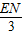 =
= ,解得:EN=
,解得:EN= ,
, 代入y=
代入y= x+1.5得:x=-
x+1.5得:x=- ,则E的坐标是:(-
,则E的坐标是:(- ,
, ),
),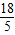 ,-
,- );
);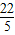 ,
,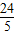 )或(-
)或(-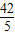 ,-
,-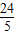 ).
).

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源:2010年重庆市江津区重点中学升学数学中考模拟试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2010年上海市徐汇区中考数学二模试卷(解析版) 题型:解答题
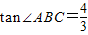 ,直线MN是梯形的对称轴,点P是线段MN上一个动点(不与M、N重合),射线BP交线段CD于点E,过点C作CF∥AB交射线BP于点F.
,直线MN是梯形的对称轴,点P是线段MN上一个动点(不与M、N重合),射线BP交线段CD于点E,过点C作CF∥AB交射线BP于点F.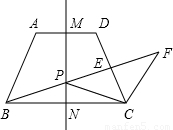
查看答案和解析>>
科目:初中数学 来源:2010年上海市徐汇区中考数学二模试卷(解析版) 题型:填空题
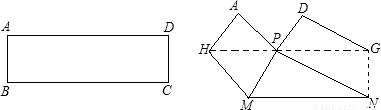
查看答案和解析>>
科目:初中数学 来源:2010年上海市徐汇区中考数学二模试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com