
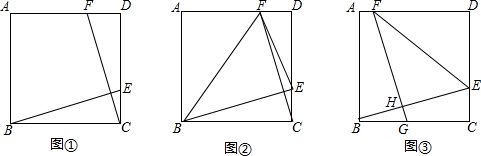
分析 (1)①连接BF,点P是两组对应点中垂线的交点.
②首先根据全等三角形的判定方法,判断出Rt△FDC≌Rt△ECB,即可推得FD=EC;然后设EC=x,则FD=x,DE=4-x,求出S△FBE关于x的解析式;最后根据△FBE的面积等于7,求出CE的长是多少即可.
(2)首先作BM∥EF,BM=EF,连接MF,作CN∥GF,判断出FG=NC,再根据Rt△NDC≌Rt△ECB,判断出NC=EB,推得FG=EB;然后判断出四边形MBEF是平行四边形,推得MF=EB,再根据∠FHE=90°,MF∥BE,可得∠MFG=90°,所以MF2+FG2=MG2,即${MG}^{2}={2FG}^{2},MG=\sqrt{2}FG$,据此判断出$EF+BG>\sqrt{2}BE$;最后判断出若点F与点A重合,点E与点D重合时,EF$+BG=BM+BG=\sqrt{2}FG=\sqrt{2}BE$,推得EF+BG与$\sqrt{2}$BE的大小关系即可.
解答 解:(1)①如图①,连接BF,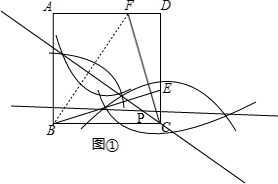 .
.
②如图②,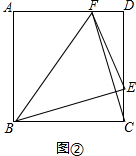 ,
,
在正方形ABCD中,AB=AD=DC=BC,
在Rt△FDC和Rt△ECB中,
$\left\{\begin{array}{l}{CF=BE}\\{DC=CB}\end{array}\right.$(HL)
∴Rt△FDC≌Rt△ECB,
∴FD=EC,
设EC=x,则FD=x,DE=4-x,
∴S△FBE=S四边形FDCB-S△FDE-S△EBC
=$\frac{4(x+4)}{2}-\frac{(4-x)x}{2}-\frac{4x}{2}$
=$\frac{1}{2}$x2-2x+8
若△FBE的面积等于7,
则$\frac{1}{2}$x2-2x+8=7,
解得${x}_{1}=2+\sqrt{2}$,${x}_{2}=2-\sqrt{2}$,
即CE的长是2$+\sqrt{2}$或2-$\sqrt{2}$.
(2)如图③,作BM∥EF,BM=EF,连接MF,作CN∥GF,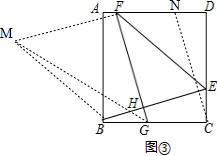 ,
,
∵FN∥CG,CN∥GF,
∴四边形FGCN为平行四边形,
∴FG=NC,
由(1),可得
Rt△NDC≌Rt△ECB,
∴NC=EB,
∴FG=EB,
∵BM∥EF,BM=EF,
∴四边形MBEF是平行四边形,
∴MF=EB,
∴MF=FG,
又∵∠FHE=90°,MF∥BE,
∴∠MFG=90°,
∴MF2+FG2=MG2,
即${MG}^{2}={2FG}^{2},MG=\sqrt{2}FG$,
∵BM=EF,
∴EF+BG=BM+BG,
在△MBG中,BM+BG>MG,
即EF$+BG>\sqrt{2}FG$,
∴$EF+BG>\sqrt{2}BE$,
若点F与点A重合,点E与点D重合时,
EF$+BG=BM+BG=\sqrt{2}FG=\sqrt{2}BE$,
综上,可得
EF+BG≥$\sqrt{2}$BE.
点评 (1)此题主要考查了四边形综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握.
(3)此题还考查了直角三角形的性质和应用,以及勾股定理的应用,要熟练掌握.


科目:初中数学 来源: 题型:填空题
 如图是用8m长的铝合金制成的矩形窗框,窗框的下部是一个正方形,上部是一个长方形,若要使窗户的透光面积为$\frac{8}{3}$m2,则窗框的高2m.
如图是用8m长的铝合金制成的矩形窗框,窗框的下部是一个正方形,上部是一个长方形,若要使窗户的透光面积为$\frac{8}{3}$m2,则窗框的高2m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
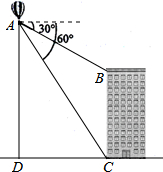 热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处于地面距离为420米,求这栋楼的高度.
热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处于地面距离为420米,求这栋楼的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
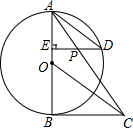 如图,AB是⊙O的直径,BC切⊙O于点B,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC,与DE交于点P.求证:
如图,AB是⊙O的直径,BC切⊙O于点B,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC,与DE交于点P.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
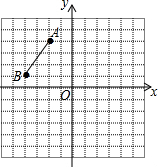 如图,在平面直角坐标系中,A(-2,4),B(-4,1),将线段AB向右平移5个单位、再向下平移1个单位得线段A1B1;将线段A1B1绕原点O旋转180°得线段A2B2,
如图,在平面直角坐标系中,A(-2,4),B(-4,1),将线段AB向右平移5个单位、再向下平移1个单位得线段A1B1;将线段A1B1绕原点O旋转180°得线段A2B2,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
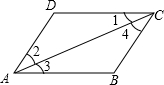 如图所示,下列推理及所注理由正确的是( )
如图所示,下列推理及所注理由正确的是( )| A. | 因为∠1=∠3,所以AB∥CD(两直线平行,内错角相等) | |
| B. | 因为AB∥CD,所以∠2=∠4(两直线平行,内错角相等) | |
| C. | 因为AD∥BC,所以∠3=∠4(两直线平行,内错角相等) | |
| D. | 因为∠2=∠4,所以AD∥BC(内错角相等,两直线平行) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com