
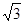 ︰2 B. 1︰3 C. 2︰3 D.
︰2 B. 1︰3 C. 2︰3 D. 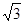 ︰3
︰3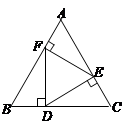
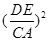 ,
,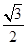 DC,EC=cos∠C×DC=
DC,EC=cos∠C×DC= 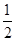 DC,
DC,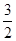 DC,
DC,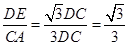 ,
,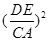 =
=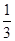 =1:3.
=1:3.

科目:初中数学 来源:不详 题型:解答题
 中,
中,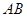 、
、 、
、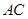 三边的长分别为
三边的长分别为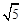 、
、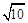 、
、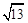 ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点 (即
(即 三个顶点都在小正方形的顶点处),如图①所示.这样不需求
三个顶点都在小正方形的顶点处),如图①所示.这样不需求 的高,而借用网格就能计算出它的面积.
的高,而借用网格就能计算出它的面积. 的面积直接填写在横线上._________________________思维拓展:
的面积直接填写在横线上._________________________思维拓展: 面积的方法叫做构图法.若
面积的方法叫做构图法.若 三边的长分别为
三边的长分别为 、
、 、
、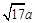 (
(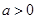 ),请利用图②的正方形网格(每个小正方形的边长为
),请利用图②的正方形网格(每个小正方形的边长为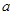 )画出相应的
)画出相应的 ,并求出它的面积.探索创新:
,并求出它的面积.探索创新: 三边的长分别为
三边的长分别为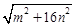 、
、 、
、 (
( ,且
,且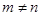 ),试运用构图法求出这三角形的面积.
),试运用构图法求出这三角形的面积.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
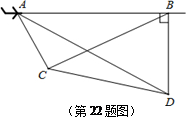
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
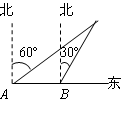
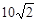 海里.求:
海里.求:
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 交AC于点E,F是
交AC于点E,F是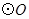 上的点,且AF=BF.
上的点,且AF=BF. 
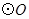 的切线;
的切线; 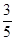 ,AE=
,AE=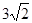 ,求sinF的值和AF的长.
,求sinF的值和AF的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com