
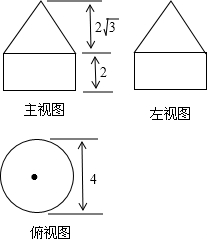
 如图是一个几何体的三视图,试描绘出这个零件的形状,并求出此三视图所描述的几何体的表面积.
如图是一个几何体的三视图,试描绘出这个零件的形状,并求出此三视图所描述的几何体的表面积. 分析 由三视图知几何体是一个组合体,上面是一个圆锥,圆锥的底面直径是4,圆锥的高是 2$\sqrt{3}$,在轴截面中圆锥的母线长使用勾股定理做出的,写出表面积,下面是一个圆柱,圆柱的底面直径是4,圆柱的高是2,做出圆柱的表面积,注意不包括重合的平面.
解答 解:由三视图知几何体是一个组合体,
上面是一个圆锥,圆锥的底面直径是4,圆锥的高是2$\sqrt{3}$,
∴在轴截面中圆锥的母线长是$\sqrt{12+{2}^{2}}$=4,
∴圆锥的侧面积是π×2×4=8π,
下面是一个圆柱,圆柱的底面直径是4,
圆柱的高是2,
∴圆柱表现出来的表面积是π×22+2π×2×2=12π
∴空间组合体的表面积是8π+12π=20π.
点评 本题考查由三视图还原几何体并且求几何体的表面积,本题解题的关键是看出图形是一个组合体,易错点可能是两个几何体重叠的部分忘记去掉,求表面积就有这样的弊端,本题是一个基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
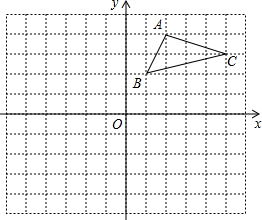 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com