练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某篮球队对队员进行定点投篮测试，每人每天投篮10次，现对甲、乙两名队员在五天中进球数（单位：个）进行统计，结果如下：

    甲

    10

    6

    10

    6

    8

    乙

    7

    9

    7

    8

    9

    经过计算，甲进球的平均数为8，方差为3.2.

    （1）求乙进球的平均数和方差；

    （2）如果综合考虑平均成绩和成绩稳定性两方面的因素，从甲、乙两名队员中选出一人去参加定点投篮比赛，应选谁？为什么？

    【答案】（1）乙平均数为8，方差为0.8；（2）乙．

    【解析】

    （1）根据平均数、方差的计算公式计算即可；

    （2）根据平均数相同时，方差越大，波动越大，成绩越不稳定；方差越小，波动越小，成绩越稳定进行解答．

    （1）乙进球的平均数为：（7+9+7+8+9）÷5=8，乙进球的方差为：[（7﹣8）2+（9﹣8）2+（7﹣8）2+（8﹣8）2+（9﹣8）2]=0.8；

    （2）∵二人的平均数相同，而S甲2=3.2，S乙2=0.8，∴S甲2＞S乙2，∴乙的波动较小，成绩更稳定，∴应选乙去参加定点投篮比赛．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知分别是的内角平分线，过点作；垂足分别为连结若则的长等于_______(用含的代数式表示结果)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．

    小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC．

    (1)按小明的思路，易求得∠APC的度数为_____度；

    (2)问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；

    (3)在(2)的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校九年级组织有奖知识竞赛，派小明去购买A、B两种品牌的钢笔作为奖品．已知一支A品牌钢笔的价格比一支B品牌钢笔的价格多5元，且买100元A品牌钢笔与买50元B品牌钢笔数目相同．

    （1）求A、B两种品牌钢笔的单价分别为多少元？

    （2）根据活动的设奖情况，决定购买A、B两种品牌的钢笔共100支，如果设购买A品牌钢笔的数量为n支，购买这两种品牌的钢笔共花费y元．

    ①直接写出y（元）关于n（支）的函数关系式；

    ②如果所购买A品牌钢笔的数量不少于B品牌钢笔数量的，请你帮助小明计算如何购买，才能使所花费的钱最少？此时花费是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

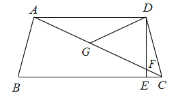
    【题目】如图，在四边形 ABCD 中，AD∥BC，DE⊥BC，垂足为点 E，连接 AC 交DE 于点 F，点 G 为 AF 的中点，∠ACD=2∠ACB，若 DC=5，则 AF 的长为___________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

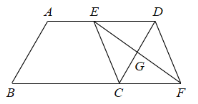
    【题目】如图，平行四边形 ABCD 中，AB=8 cm，BC=12 cm，∠B=60°，G 是CD 的中点，E 是边 AD 上的动点，EG 的延长线与 BC 的延长线交于点 F， 连接 CE，DF．

    （1）求证：四边形 CEDF 是平行四边形；

    （2）①AE= cm 时，四边形 CEDF 是矩形，请写出判定矩形的依据（一条即可）；

    ②AE= cm 时，四边形 CEDF 是菱形，请写出判定菱形的依据（一条即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数

    （1）若函数图像经过原点，求m的值；

    （2）若这个函数是一次函数，且与y轴交点为（0，3），求该一次函数图像与两坐标轴围成的三角形的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：直线AB∥CD，点M，N分别在直线AB，CD上，点E为平面内一点.

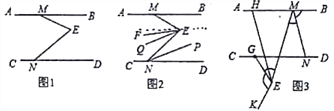
    (1)如图1，∠BME，∠E，∠END的数量关系为 (直接写出答案)；

    (2)如图2，∠BME＝m°，EF平分∠MEN，NP平分∠END，EQ∥NP，求∠FEQ的度数(用用含m的式子表示)

    (3)如图3，点G为CD上一点，∠BMN＝n·∠EMN，∠GEK＝n·∠GEM，EH∥MN交AB于点H，探究∠GEK，∠BMN，∠GEH之间的数量关系(用含n的式子表示)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

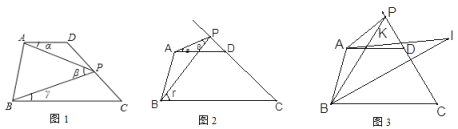
    【题目】如图，已知四边形ABCD，AD∥BC．点P在直线CD上运动（点P和点C，D不重合，点P，A，B不在同一条直线上），若记∠DAP，∠APB，∠PBC分别为∠α，∠β，∠γ．

    （1）如图1，当点P在线段CD上运动时，写出∠α，∠β，∠γ之间的关系并说出理由；

    （2）如图2，如果点P在线段CD的延长线上运动，探究∠α，∠β，∠γ之间的关系，并说明理由．

    （3）如图3，BI平分∠PBC，AI交BI于点I，交BP于点K，且∠PAI：∠DAI=5：1，∠APB=20°，∠I=30°，求∠PAI的度数．

    查看答案和解析>>

    同步练习册答案