
分析 (1)根据方程有两个不相等的实数根结合根的判别式即可得出△=8k+1>0,解不等式即可得出k的取值范围;
(2)将x=2代入原方程可得出(k+2)2+1=0,由该方程无解即可得出结论.
解答 解:(1)∵方程2x2+(4k+1)x+2k2=0有两个不相等的实数根,
∴△=(4k+1)2-4×2×2k2=8k+1>0,
解得:k>-$\frac{1}{8}$.
(2)将x=2代入原方程得:2×22+2×(4k+1)+2k2=0,
化简得:k2+4k+5=0,即(k+2)2+1=0,
∵此方程无解,
∴无论k取何值,x=2都不可能是原方程的根.
点评 本题考查了根的判别式,根据根的判别式得出关于k的一元一次不等式是解题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
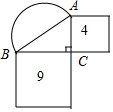 如图,在Rt△ABC中,∠ACB=90°,分别以AC和BC为边长的两个正方形面积分别为4和9,则以AB长为直径的半圆的面积为$\frac{13π}{8}$.
如图,在Rt△ABC中,∠ACB=90°,分别以AC和BC为边长的两个正方形面积分别为4和9,则以AB长为直径的半圆的面积为$\frac{13π}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com