
分析 如图,AC=4×0.5m=2m,CE=5×0.5m=2.5m,AB=CD=1.6m,先证明△CAB∽△COP,利用相似比得到$\frac{1.6}{OP}$=$\frac{2}{2+AO}$①,再证明△ECD∽△EOP得到$\frac{1.6}{OP}$=$\frac{2.5}{2.5+2+AO}$②,然后解关于OP和AO的方程组求出OP即可.
解答 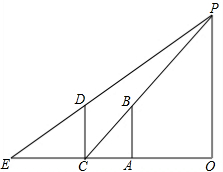 解:如图,AC=4×0.5m=2m,CE=5×0.5m=2.5m,AB=CD=1.6m,
解:如图,AC=4×0.5m=2m,CE=5×0.5m=2.5m,AB=CD=1.6m,
∵AB∥OP,
∴△CAB∽△COP,
∴$\frac{AB}{OP}$=$\frac{CA}{CO}$,即$\frac{1.6}{OP}$=$\frac{2}{2+AO}$①,
∵CD∥OP,
∴△ECD∽△EOP,
∴$\frac{CD}{OP}$=$\frac{EC}{EO}$,即$\frac{1.6}{OP}$=$\frac{2.5}{2.5+2+AO}$②,
由①②得$\frac{2}{2+AO}$=$\frac{2.5}{2.5+2+AO}$,解得AO=8,
∴$\frac{1.6}{OP}$=$\frac{2}{2+8}$,解得OP=8.
答:路灯的高度为8m.
点评 本题考查了相似三角形的应用:借助标杆或直尺测量物体的高度,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
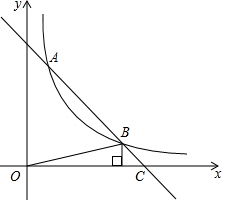 如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴相交于点C,△BOC的面积为$\frac{5}{2}$.
如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴相交于点C,△BOC的面积为$\frac{5}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com