
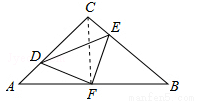
(9分)如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中
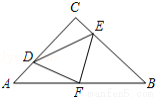
(1)求证:△DFE是等腰直角三角形.
(2)求DE长度的最小值.
(3)求△CDE面积的最大值.
(1)证明见试题解析;(2)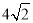 ;(3)8.
;(3)8.
【解析】
试题分析:(1)连接CF,由SAS定理可得△CFE≌△ADF,从而可证∠DFE=90°可得DF=EF,可得△DFE是等腰直角三角形;
(2)由DE=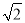 DF,当DF最小时,DE也最小,而当DF⊥AC时,DF最小,DE取最小值
DF,当DF最小时,DE也最小,而当DF⊥AC时,DF最小,DE取最小值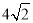 ;
;
(3)由△ADF≌△CEF,得到S△CEF=S△ADF,故S四边形CDFE=S△DCF+S△CEF=S△DCF+S△ADF=S△ACF=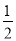 S△ABC,当△DEF的面积最小时,△CED面积最大,S△CED=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8.
S△ABC,当△DEF的面积最小时,△CED面积最大,S△CED=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8.
试题解析:(1)连接CF,∵△ABC为等腰直角三角形,∴∠FCB=∠A=45°,CF=AF=FB,∵AD=CE,∴△ADF≌△CEF,∴EF=DF,∠CFE=∠AFD,∵∠AFD+∠CFD=90°,∴∠CFE+∠CFD=∠EFD=90°,∴△EDF是等腰直角三角形;
(2)∵△DEF是等腰直角三角形,∴当DE最小时,DF也最小,即当DF⊥AC时,DE最小,此时DF=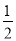 BC=4,∴DE=
BC=4,∴DE=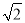 DF=
DF=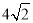 ;
;
(3)∵△ADF≌△CEF,∴S△CEF=S△ADF,∴S四边形CDFE=S△DCF+S△CEF=S△DCF+S△ADF=S△ACF=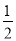 S△ABC,当△DEF的面积最小时,△CED面积最大,S△CED=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8.
S△ABC,当△DEF的面积最小时,△CED面积最大,S△CED=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8.
考点:1.等腰直角三角形;2.全等三角形的判定与性质.
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.

科目:初中数学 来源:2014-2015学年江苏省南通市崇川区九年级3月月考数学试卷(解析版) 题型:填空题
据2014年南通市统计的全市在籍总人口数约为7700000人,把“7700000”用科学记数法表示应为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省丹阳市十乡九年级下学期第一次联考数学试卷(解析版) 题型:填空题
读取表格中的信息,解决问题.满足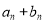 >1000的n可以取得的最小正整数是 .
>1000的n可以取得的最小正整数是 .
n=1 |
|
|
n=2 |
|
|
n=3 |
|
|
… | … | … |
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省丹阳市十乡九年级下学期第一次联考数学试卷(解析版) 题型:填空题
如图,CD是△ABC的中线,点E、F分别是AC、DC的中点,EF=1,则BD .
.
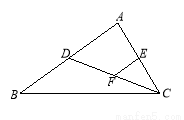
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省邯郸市九年级第一次模拟考试数学试卷(解析版) 题型:解答题
(本小题满分11分)如图1,在△ABC中,∠ACB=90°,AC=BC=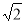 ,以点B为圆心,以1为半径作圆. 设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA,PD,PB,
,以点B为圆心,以1为半径作圆. 设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA,PD,PB,

(1)求证:AD=BP;
(2)若DP与⊙B相切,则∠CPB的度数为_________°;
(3)如图2,当B,P,D三点在同一直线上时,求BD的长;
(4)BD的最小值为________,此时tan∠CBP=_________;BD的最大值为 ,此时tan∠CPB=_________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:选择题
已知二次函数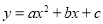 (
( )的图象如图所示,下列说法错误的是( )
)的图象如图所示,下列说法错误的是( )
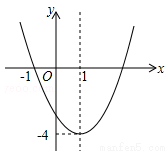
A.二次函数的图象关于直线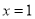 对称
对称
B.当 时,y随x的增大而减小
时,y随x的增大而减小
C.-1和3是方程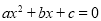 (
( )的两个根
)的两个根
D.函数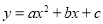 (
( )的最小值是
)的最小值是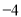
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com