
如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.
(1)求证:① PE=PD ; ② PE⊥PD;
(2)设AP=x, △PBE的面积为y.
① 求出y关于x的函数关系式,并写出x的取值范围;
② 当x取何值时,y取得最大值,并求出这个最大值.
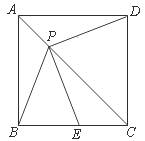
(1)证法一:
① ∵ 四边形ABCD是正方形,AC为对角线,
∴ BC=DC, ∠BCP=∠DCP=45°.
∵ PC=PC,
∴ △PBC≌△PDC (SAS).
∴ PB= PD, ∠PBC=∠PDC.
又∵ PB= PE ,
∴ PE=PD.
② (i)当点E在线段BC上(E与B、C不重合)时,
∵ PB=PE,
∴ ∠PBE=∠PEB,
∴ ∠PEB=∠PDC,
∴ ∠PEB+∠PEC=∠PDC+∠PEC=180°,
∴ ∠DPE=360°-(∠BCD+∠PDC+∠PEC)=90°,
∴ PE⊥PD.
(ii)当点E与点C重合时,点P恰好在AC中点处,此时,PE⊥PD.
(iii)当点E在BC的延长线上时,如图.
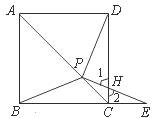
∵ ∠PEC=∠PDC,∠1=∠2,
∴ ∠DPE=∠DCE=90°,
∴ PE⊥PD.
综合(i)(ii)(iii), PE⊥PD
(2)① 过点P作PF⊥BC,垂足为F,则BF=FE.
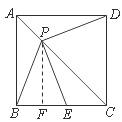
∵ AP=x,AC=![]() ,
,
∴ PC=![]() - x,PF=FC=
- x,PF=FC=![]() .
.
BF=FE=1-FC=1-(![]() )=
)=![]() .
.
∴ S△PBE=BF?PF=![]() (
(![]() )
)![]() .
.
即 ![]() (0<x<
(0<x<![]() ).
).
② ![]() .
.
∵ ![]() <0,
<0,
∴ 当![]() 时,y最大值
时,y最大值![]() .
.
(1)证法二:① 过点P作GF∥AB,分别交AD、BC于G、F. 如图所示.
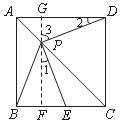
∵ 四边形ABCD是正方形,
∴ 四边形ABFG和四边形GFCD都是矩形,
△AGP和△PFC都是等腰直角三角形.
∴ GD=FC=FP,GP=AG=BF,∠PGD=∠PFE=90°.
又∵ PB=PE,
∴ BF=FE,
∴ GP=FE,
∴ △EFP≌△PGD (SAS).
∴ PE=PD.
② ∴ ∠1=∠2.
∴ ∠1+∠3=∠2+∠3=90°.
∴ ∠DPE=90°.
∴ PE⊥PD.
(2)①∵ AP=x,
∴ BF=PG=![]() ,PF=1-
,PF=1-![]() .
.
∴ S△PBE=BF?PF=![]() (
(![]() )
)![]() .
.
即 ![]() (0<x<
(0<x<![]() ).
).
② ![]() .
.
∵ ![]() <0,
<0,
∴ 当![]() 时,y最大值
时,y最大值![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )
14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com