
【题目】如图,在四边形ABCD中,AB=BC , 对角线BD平分∠ABC , P是BD上一点,过点P作PM⊥AD , PN⊥CD , 垂足分别为M , N . 
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
【答案】
(1)
解答:证明:∵对角线BD平分∠ABC,∴∠ABD=∠CBD,在△ABD和△CBD中, 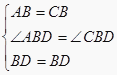 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB.
(2)
解答:证明:∵PM⊥AD,PN⊥CD
∴∠PMD=∠PND=90°,∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°,
∴PM=MD,
∴四边形MPND是正方形.
【解析】(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD , 由全等三角形的性质即可得到:∠ADB=∠CDB;(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】今年,我国部分地区“登革热”流行,党和政府采取果断措施,防治结合,防止病情继续扩散.如图是某同学记载的9月1日至30日每天某地的“登革热”新增确诊病例数据日.将图中记载的数据每5天作为一组,从左至右分为第一组至第六组,下列说法:①第一组的平均数最大,第六组的平均数最小;②第二组的中位数为146;③第四组的众数为28.其中正确的有( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题:
(1)分解因式:4a2﹣8ab+4b2﹣16c2
(2)计算:(2a+b)(2a﹣b)+b(2a+b)﹣8a2b÷2b
(3)化简求值:( ![]() ﹣
﹣ ![]() )÷
)÷ ![]() ,其中x=﹣3
,其中x=﹣3
(4)解分式方程: ![]() ﹣1=
﹣1= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的方程x2﹣2x+n=0无实数根,则一次函数y=(n﹣1)x﹣n的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D在AB上,E在AC上,且∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( ) 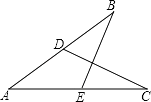
A.AD=AE
B.∠AEB=∠ADC
C.BE=CD
D.AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB , D为AB边上一点,过点D作DE⊥BC , 交直线MN于E , 垂足为F , 连CD、BE . 
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.

(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?若变化,说明理由;若不变,求∠DOE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com