
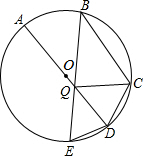
 如图,已知A、B、C、D是⊙O上四点,点E在弧AD上,连接BE交AD于点Q,若∠AQE=∠EDC,∠CQD=∠E,求证:AQ=BC.
如图,已知A、B、C、D是⊙O上四点,点E在弧AD上,连接BE交AD于点Q,若∠AQE=∠EDC,∠CQD=∠E,求证:AQ=BC. 分析 首先根据圆周角定理,可得∠A=∠E,再根据∠CQD=∠E,可得∠CQD=∠A,所以AB∥CQ;然后根据圆内接四边形的性质,以及∠AQE=∠EDC,判断出BC∥AQ,即可判断出四边形ABCQ是平行四边形,所以AQ=BC,据此解答即可.
解答 证明:如图: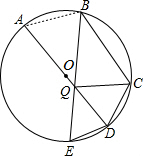 ,
,
根据圆周角定理,可得∠A=∠E,
∵∠CQD=∠E,
∴∠CQD=∠A,
∴AB∥CQ,
∵∠EBC+∠EDC=180°,∠AQB+∠AQE=180°,
∴∠EBC+∠EDC=∠AQB+∠AQE,
∵∠AQE=∠EDC,
∴∠EBC=∠AQB,
∴BC∥AQ,
又∵AB∥CQ,
∴四边形ABCQ是平行四边形,
∴AQ=BC.
点评 (1)此题主要考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
(2)此题还考查了平行四边形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确平行四边形的判定方法,以及平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分.
(3)此题还考查了圆内接四边形的性质,要熟练掌握,解答此题的关键是要明确:①圆内接四边形的对角互补. ②圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角).


科目:初中数学 来源: 题型:选择题
| 身高(厘米) | 159 | 160 | 162 | 165 | 167 | 168 |
| 人数 | 3 | 5 | 8 | 18 | 10 | 8 |
| A. | 159 | B. | 162 | C. | 165 | D. | 167 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
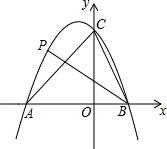 如图,二次函数y=-x2-x+6的图象与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,点P是该图象上一点,且满足∠ABP=∠ACB,则点P的坐标是(-2,4)或(-4,-6).
如图,二次函数y=-x2-x+6的图象与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,点P是该图象上一点,且满足∠ABP=∠ACB,则点P的坐标是(-2,4)或(-4,-6).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
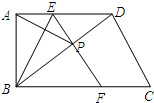 如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E为边AD上一点,将△ABE沿直线BE折叠,使A点落在四边形对角线BD上的P点处,EP的延长线交直线BC于点F.设AD=a,AB=b,BC=c.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E为边AD上一点,将△ABE沿直线BE折叠,使A点落在四边形对角线BD上的P点处,EP的延长线交直线BC于点F.设AD=a,AB=b,BC=c.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
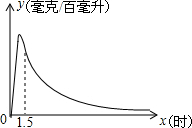 实验数据显示:一般成人喝半斤低度白酒后,其血液中酒精含量y(毫克/百毫升)与时间x(小时)的关系为:当0≤x≤1.5时,y与x成二次函数关系,即y=-200x2+400x;当x≥1.5时,y与x成反比例函数关系,即y=$\frac{k}{x}$.
实验数据显示:一般成人喝半斤低度白酒后,其血液中酒精含量y(毫克/百毫升)与时间x(小时)的关系为:当0≤x≤1.5时,y与x成二次函数关系,即y=-200x2+400x;当x≥1.5时,y与x成反比例函数关系,即y=$\frac{k}{x}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com