
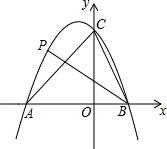
 如图,二次函数y=-x2-x+6的图象与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,点P是该图象上一点,且满足∠ABP=∠ACB,则点P的坐标是(-2,4)或(-4,-6).
如图,二次函数y=-x2-x+6的图象与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,点P是该图象上一点,且满足∠ABP=∠ACB,则点P的坐标是(-2,4)或(-4,-6). 分析 认真审题,首先过点C作CQ∥PB,利用△ACB∽△AQC,求出点Q的坐标,再求出直线PB的解析式,进而得解.
解答 解:当-x2-x+6=0时,
x=2或x=-3,
∵A在B的左侧,
∴A(-3,0),B(2,0),
当x=0时,y=6,
∴C(0,6),
Rt△AOC中,AO=3,CO=6,
AC=$\sqrt{A{O}^{2}+C{O}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,
如图,过点C作CQ∥PB,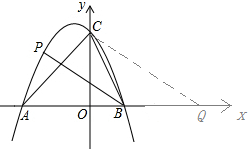
∴∠ABP=∠AQC,
∵∠ABP=∠ACB,
∴∠ACB=∠AQC,
又∵∠CAB=∠CAQ,
∴△ACB∽△AQC,
∴$\frac{AC}{AQ}=\frac{AB}{AC}$,
即:AB•AQ=AC2,
设BO=x,
则:AQ=OA+OB=3+x,
AB=3+2=5,
∴45=5(3+x),
解得:x=6,
∴Q(6,0),
设直线CQ的解析式为:y=kx+b,
把点C(0,6)和点Q(6,0)代入可得:
$\left\{\begin{array}{l}{b=6}\\{6k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=6}\end{array}\right.$,
∴直线CQ的解析式为:y=-x+6,
∴可设直线PB的解析式为:y=-x+c,
把点B(2,0)代入可得:0=-2+c,
解得:c=2,
∴直线PB的解析式为:y=-x+2,
∴$\left\{\begin{array}{l}{y=-x+2}\\{y=-{x}^{2}-x+6}\end{array}\right.$,
解得:x=-2或x=2(舍),
∴点P(-2,4).
由对称性可知,(-4,-6)也是符号要求的点,
故答案为(-2,4)或(-4,-6).
点评 本题主要考查了相似三角形与二次函数结合的问题,以及直线的解析式的求法,是综合性比较强的题目,注意认真总结.


科目:初中数学 来源: 题型:填空题
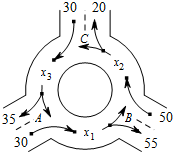 如图为某三岔路口交通环岛的简化模型.在某高峰时段,单位时间进出路口A,B,C的机动车辆数如图所示,图中x1,x2,x3分别表示该时段单位时间通过路段$\widehat{AB}$,$\widehat{BC}$,$\widehat{CA}$的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则x1,x2,x3的大小关系是x3>x1>x2.(用“>”、“<”或“=”连接)
如图为某三岔路口交通环岛的简化模型.在某高峰时段,单位时间进出路口A,B,C的机动车辆数如图所示,图中x1,x2,x3分别表示该时段单位时间通过路段$\widehat{AB}$,$\widehat{BC}$,$\widehat{CA}$的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则x1,x2,x3的大小关系是x3>x1>x2.(用“>”、“<”或“=”连接)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
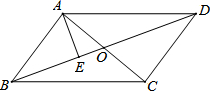 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AE⊥BD于点E.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AE⊥BD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{25}{12}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
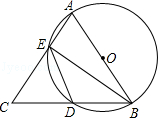 如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.
如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 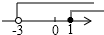 | B. | 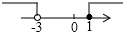 | C. |  | D. | 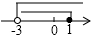 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com