①已知将不等式mx>m的两边都除以m,得x<1,则m应满足________,
②当m>2时,不等式(2-m)x<8的解集为________.
③已知(-m2-1)x>1,则x________.
m<0

<
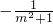
分析:(1)将不等式mx>m的两边都除以m,得x<1,即不等号的方向改变,那么除以的是负数,∴m<0;
(2)当m>2时,即(m-2)<0,两边都除以负数,不等号的方向改变,不等式(2-m)x<8的解集为x>
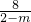
;
(3)(-m
2-1)=-(m
2+1)<0,两边都除以负数,不等号的方向改变,则其解集为x<
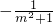
.
解答:(1)m<0;
(2)x>
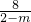
;
(3)<
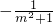
.
点评:主要考查不等式的性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
