练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    计算：-12014+|-
    1
    2
    |-sin45°．
    考点：实数的运算,特殊角的三角函数值
    专题：计算题
    分析：原式第一项利用乘方的意义化简，第二项利用绝对值的代数意义化简，最后一项利用特殊角的三角函数值计算即可得到结果．
    解答：解：原式=-1+
    		2
    2
    -
    		2
    2
    =-1．
    点评：此题考查了实数的运算，以及特殊角的三角函数值，熟练掌握运算法则是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    一个不透明的袋里装有5个球，其中2个红球，3个白球，它们除颜色外其余都相同．
    （1）求摸出1个球是白球的概率；
    （2）求一次摸出一个球不放回，再摸出一个球，两次都是红球的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

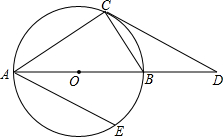    如图所示，△ABC内接于⊙O，AB是⊙O的直径，D是AB延长线上一点，连接DC，且AC=DC，BC=BD．
    （1）求证：DC是⊙O的切线；
    （2）作CD的平行线AE交⊙O于点E，已知DC=10
    		3
    ，求圆心O到AE的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在绿化某县城与高速公路的连接路段时，需计划购买罗汉松、雪松两种树苗共400株，罗汉松树苗每株60元，雪松树苗每株70元．相关资料表明：罗汉松、雪松树苗的成活率分别为70%、90%．
    （1）若购买这两种树苗共用去26500元，则罗汉松、雪松树苗各购买多少株？
    （2）绿化工程在来年一般都要将死树补上新树苗，现要使这两种树苗在来年共补苗不多于80株，则罗汉松树苗至多购买多少株？
    （3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？请求出最低费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在等边△ABC中，以BC为直径的⊙O与AB交于点D，DE⊥AC，垂足为点E．
    （1）求证：DE为⊙O的切线；
    （2）计算
    CE
    AE
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图⊙O的半径为1cm，弦AB、CD的长度分别为
    		2
    cm，1cm，
    （1）求圆心O到弦AB的距离；
    （2）则弦AC、BD所夹的锐角α的度数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

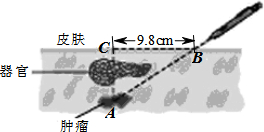    如图，一名患者体内某重要器官后面有一肿瘤在A处．在接受放射性治疗时，为了最大限度地保证疗效，并且防止伤害器官，射线必须从侧面照射肿瘤．已知射线与皮肤的夹角∠CBA为32°44′，射线从肿瘤右侧9.8cm的B处进入身体，求肿瘤在皮下的深度（精确到0.1cm）．
    [参考数据：sin32°44′≈0.54，cos32°44′≈0.84，tan32°44′≈0.64]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标中，点O为坐标原点，直线y=-x+4与x轴交于点A，过点A的抛物线y=ax2+bx与直线y=-x+4交于另一点B，且点B的横坐标为1．

    （1）求a，b的值；
    （2）点P是线段AB上一动点（点P不与点A、B重合），过点P作PM∥OB交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，过点P作PF⊥MC于点F，设PF的长为t，MN的长为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；
    （3）在（2）的条件下，当S△ACN=S△PMN时，连接ON，点Q在线段BP上，过点Q作QR∥MN交ON于点R，连接MQ、BR，当∠MQR-∠BRN=45°时，求点R的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

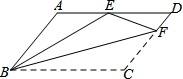    如图，点F为?ABCD的CD边上一点，将△BCF沿BF折起，点C恰好落在AD边上的E点处，△ABE和△DEF的周长分别为10和7，则?ABCD的周长为
     
    ．

    查看答案和解析>>

    同步练习册答案