
|
|


科目:初中数学 来源: 题型:
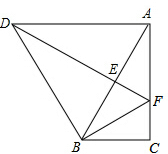 如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.
如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.查看答案和解析>>
科目:初中数学 来源: 题型:
 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 某花店计划下个月每天购进80只玫瑰花进行销售,若下个月按30天计算,每售出1只玫瑰花获利润5元,未售出的玫瑰花每只亏损3元.以x(0<x≤80)表示下个月内每天售出的只数,y(单位:元)表示下个月每天销售玫瑰花的利润.根据历史资料,得到同期下个月内市场销售量的频率分布直方图(每个组距包含左边的数,但不包含右边的数)如图所示:
某花店计划下个月每天购进80只玫瑰花进行销售,若下个月按30天计算,每售出1只玫瑰花获利润5元,未售出的玫瑰花每只亏损3元.以x(0<x≤80)表示下个月内每天售出的只数,y(单位:元)表示下个月每天销售玫瑰花的利润.根据历史资料,得到同期下个月内市场销售量的频率分布直方图(每个组距包含左边的数,但不包含右边的数)如图所示:| 销售量/只 | 70 | 72 | 74 | 75 | 77 | 79 |
| 天数 | 1 | 2 | 3 | 4 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,平行四边形OABC的点C在x轴上,点A在直线y=x上,点B在双曲线y=
已知,如图,平行四边形OABC的点C在x轴上,点A在直线y=x上,点B在双曲线y=| k |
| x |
| OA |
| OC |
| 1 | ||
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com