
【题目】如图,⊙![]() 是
是![]() 的外接圆,直线
的外接圆,直线![]() 与
与![]() 相切于点
相切于点![]() ,且
,且![]() .
.

(![]() )求证:
)求证: ![]() 平分
平分![]() .
.
(![]() )作
)作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)连接OD,由直线l与⊙O相切于点D可得出OD⊥l,结合l∥BC即可得出OD⊥BC,再根据垂径定理即可得出弧BD=弧CD,进而可得出∠BAD=∠CAD,即AD平分∠BAC;
(2)由角平分线的定义结合(1)的结论即可得出∠CBD+∠CBE=∠BAE+∠ABE,再根据三角形外角的性质即可得出∠EBD=∠DEB,由此即可证出BD=DE.
试题解析:证明:(1)连接OD,如图所示.
∵直线l与⊙O相切于点D,∴OD⊥l.
∵l∥BC,∴OD⊥BC,∴弧BD=弧CD,∴∠BAD=∠CAD,∴AD平分∠BAC;
(2)∵BE平分∠ABC,∴∠ABE=∠CBE.
又∵弧BD=弧CD,∴∠BAD=∠CBD,∴∠CBD+∠CBE=∠BAE+∠ABE.
又∵∠DEB=BAE+∠ABE,∴∠EBD=∠DEB,∴BD=DE.



科目:初中数学 来源: 题型:
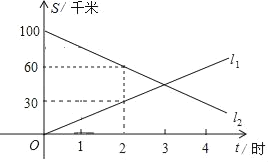
【题目】A,B两地相距100千米,甲,乙两人骑车同时分别从A、B两地相向而行,假设他们都保持匀速行驶,直线l1,l2分别表示甲,乙两人与A地的距离S(单位:km)与行驶时间t(单位:h)之间关系的图象.
根据图象提供的信息,解答下列问题:
(1)甲、乙两人的速度分别是多少?
(2)经过多长时间,两人相遇?
(3)分别写出甲,乙两人与A地的距离S(单位:km)与行驶时间t(单位:h)之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
如图①,![]() 、
、![]() 是⊙
是⊙![]() 的两条弦,
的两条弦, ![]() ,
, ![]() 是
是![]() 的中点,
的中点, ![]() ,垂足为
,垂足为![]() .
.
求证: ![]() .
.


小敏在解答此题时,利用了“补短法”进行证明,她的方法如下:
如图②,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
(请你在下面的空白处完成小敏的证明过程.)
推广运用
如图③,等边![]() 内接于⊙
内接于⊙![]() ,
, ![]() .
. ![]() 是
是![]() 上一点,
上一点, ![]() ,
, ![]() ,垂足为
,垂足为![]() ,则
,则![]() 的周长是__________.
的周长是__________.


拓展研究
如图④,若将“问题提出”中的“![]() 是
是![]() 的中点”改成“
的中点”改成“![]() 是
是![]() 的中点”,其余条件不变,“
的中点”,其余条件不变,“![]() ”这一结论还成立吗?若成立,请说明理由;若不成立,写出
”这一结论还成立吗?若成立,请说明理由;若不成立,写出![]() 、
、![]() 、
、![]() 三者之间存在的关系并说明理由.
三者之间存在的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△OBC的顶点分别为O(0,0)、B(3,-1)、C(2,1).
(1)以点O(0,0)为位似中心,按比例尺2: 1在位似中心的异侧将△OBC放大为![]() ,放大后点B、C两点的对应点分别为
,放大后点B、C两点的对应点分别为![]() 、
、![]() ,画出
,画出![]() ,并写出点为
,并写出点为![]() 、
、![]() 的坐标。
的坐标。
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点![]() 的坐标。(3)求
的坐标。(3)求![]() 的面积。
的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1,2,3三个数字.小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束后得到一组数(若指针指在分界线时重转).
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)求每次游戏后得到的一组数恰好是方程x2﹣4x+3=0的解的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是______度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com