
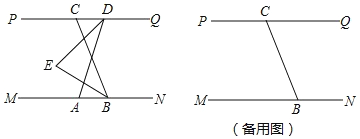
【题目】如图,已知 MN∥PQ,B 在 MN 上,C 在 PQ 上,A 在 B 的左侧,D 在 C 的右侧,DE 平分∠ADC,BE平分∠ABC,直线 DE,BE 交于点 E,∠CBN=120°.
(1)若∠ADQ=110°,求∠BED 的度数;
(2)将线段 AD 沿 DC 方向平移,使得点 D 在点 C 的左侧,其他条件不变,若∠ADQ=n°,求∠BED 的度数(用含 n 的代数式表示)
【答案】(1)65°;(2)∠BED=210°﹣(![]() n)°或(
n)°或(![]() n)°﹣30°或 30°﹣(
n)°﹣30°或 30°﹣(![]() n)°.
n)°.
【解析】(1)如图1中,延长DE交MN于H.利用∠BED=∠EHB+∠EBH,即可解决问题;
(2)分三种情形讨论即可解决问题.
(1)如图 1 中,延长 DE 交 MN 于 H.
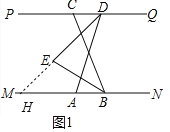
∵∠ADQ=110°,ED 平分∠ADP,
∴∠PDH=![]() ∠PDA=35°,
∠PDA=35°,
∵PQ∥MN,
∴∠EHB=∠PDH=35°,
∵∠CBN=120°,EB 平分∠ABC,
∴∠EBH=![]() ∠ABC=30°,
∠ABC=30°,
∴∠BED=∠EHB+∠EBH=65°.
(2)有 3 种情形,如图 2 中,当点 E 在直线 MN 与直线 PQ 之间时.延长 DE 交 MN 于 H.
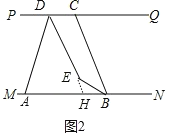
∵PQ∥MN,
∴∠QDH=∠DHA=![]() n°,
n°,
∴∠BED=∠EHB+∠EBH=180°﹣(![]() n)°+30°=210°﹣(
n)°+30°=210°﹣(![]() n)°,
n)°,
当点 E 在直线 MN 的下方时,如图 3 中,
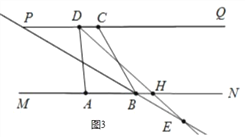
设 DE 交 MN 于 H.
∵∠PBC=∠ABP=30°,
∴∠HBE=∠ABP=30°(对顶角).
∵∠ADH=∠CDH=(![]() n)°,
n)°,
∴∠CDH=∠DHB=(![]() n)°(两直线平行,内错角相等).
n)°(两直线平行,内错角相等).
又∵∠DHB=∠HBE+∠HEB,
∴∠BED=(![]() n)°﹣30°,
n)°﹣30°,
当点 E 在 PQ 上方时,如图 4 中,
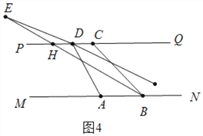
设 PQ 交 BE 于 H.同法可得∠BED=30°﹣(![]() n)°.
n)°.
综上所述,∠BED=210°﹣(![]() n)°或(
n)°或(![]() n)°﹣30°或 30°﹣(
n)°﹣30°或 30°﹣(![]() n)°.
n)°.


科目:初中数学 来源: 题型:
【题目】如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:① GA=GP;② S△PAC∶S△PAB=AC∶AB;③ BP垂直平分CE;④ FP=FC,其中正确的判断有( )
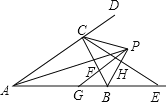
A. 只有①② B. 只有③④ C. 只有①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②a+c>b;③抛物线y=ax2+bx+c与x轴的另一个交点为(3,0);④abc>0.其中正确的结论是(填写序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面关于三角形内外角平分线的研究片断,完成所提出的问题.
探究1:如图(1)在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB.
∠ACB.
∴∠1+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
∴∠BOC=180°-(∠1+∠2)=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ∠A
∠A
探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
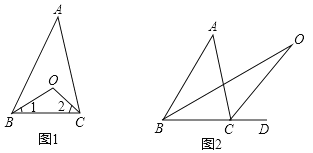
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是反比例函数
是反比例函数![]() 图像上一点,作
图像上一点,作![]() 轴于点
轴于点![]() ,且
,且![]() 的面积为
的面积为![]() ,点
,点![]() 坐标为
坐标为![]() .
.

(![]() )求
)求![]() 和
和![]() 的值.
的值.
(![]() )若直线
)若直线![]() 经过点
经过点![]() ,交另一支双曲线于点
,交另一支双曲线于点![]() ,求
,求![]() 的面积.
的面积.
(![]() )指出
)指出![]() 取何值时,一次函数的值大于反比例函数的值,直接写出结果.
取何值时,一次函数的值大于反比例函数的值,直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图2,“和谐号”高铁列车的小桌板收起时近似看作与地面垂直,展开小桌板使桌面保持水平时如图1,小桌板的边沿O点与收起时桌面顶端A点的距离OA=75厘米,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与支架长BC的长度之和等于OA的长度. 
(1)求∠CBO的度数;
(2)求小桌板桌面的宽度BC.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我中华”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,则下列说法中错误的是( )
A. 甲、乙得分的平均数都是8 B. 甲得分的众数是8,乙得分的众数是9
C. 甲得分的中位数是9,乙得分的中位数是6 D. 甲得分的方差比乙得分的方差小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com