
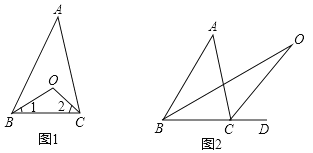
【题目】认真阅读下面关于三角形内外角平分线的研究片断,完成所提出的问题.
探究1:如图(1)在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB.
∠ACB.
∴∠1+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
∴∠BOC=180°-(∠1+∠2)=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ∠A
∠A
探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
科目:初中数学 来源: 题型:
【题目】△ABC中,AD⊥BC,AE平分∠BAC交BC于点E.
(1)∠B=30°,∠C=70°,求∠EAD的大小.
(2)若∠B<∠C,则2∠EAD与∠C-∠B是否相等?若相等,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强与小刚都住在安康小区,在同一所学校读书.某天早上,小强![]() 从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留
从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留![]() 分钟,校车行驶途中始终保持匀速.当天早上,小刚
分钟,校车行驶途中始终保持匀速.当天早上,小刚![]() 从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早
从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早![]() 分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程
分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.
(1)求点![]() 的纵坐标
的纵坐标![]() 的值;
的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD∥GE,AQ 平分∠FAC,交 BD 于 Q,∠GFA=50°,∠Q=25°,则∠ACB 的 度数( )
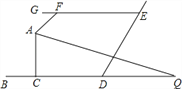
A. 90° B. 95° C. 100° D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,CE⊥AB 于 E,DF⊥AB 于 F,AC∥ED,CE 是∠ACB 的平分线, 则图中与∠FDB 相等的角(不包含∠FDB)的个数为( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
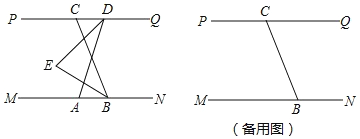
【题目】如图,已知 MN∥PQ,B 在 MN 上,C 在 PQ 上,A 在 B 的左侧,D 在 C 的右侧,DE 平分∠ADC,BE平分∠ABC,直线 DE,BE 交于点 E,∠CBN=120°.
(1)若∠ADQ=110°,求∠BED 的度数;
(2)将线段 AD 沿 DC 方向平移,使得点 D 在点 C 的左侧,其他条件不变,若∠ADQ=n°,求∠BED 的度数(用含 n 的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)如图①,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你画出以格点为顶点,OA,OB为勾股边且对角线相等的勾股四边形OAMB;


(2)如图②,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD,DC,∠DCB=30°,求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B,C重合),经过点O、P折叠该纸片,得点B′和折痕OP(如图①)经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ(如图②),当点C′恰好落在OA上时,点P的坐标是 . 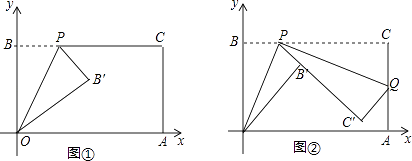
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com