
分析 根据相似三角形的性质,相似三角形(多边形)的周长的比等于相似比;相似三角形的面积的比等于相似比的平方,则△ABC和△DEF的对应高的比为3:1,周长的比为3:1,面积的比为9:1,
然后利用△ABC的周长为18,面积为27可计算出△DEF的周长和面积.
解答 解:∵△ABC∽△DEF,相似比为3:1,
∴这两个三角形对应高的比为3:1;
这两个三角形的周长的比为3:1,面积的比为9:1,
∴△DEF的周长=$\frac{1}{3}$×18=6,面积为$\frac{1}{9}$×27=3.
故答案为3:1,6,3.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等;相似三角形(多边形)的周长的比等于相似比;相似三角形的面积的比等于相似比的平方.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
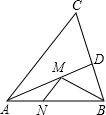 如图,在锐角△ABC中,AC=10,S△ABC=25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是5.
如图,在锐角△ABC中,AC=10,S△ABC=25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com