Question

6．我们规定：在正方形ABCD中，以正方形的一个顶点A为顶点，且过对角顶点C的抛物线，称为这个正方形的以A为顶点的对角抛物线．
（1）在平面直角坐标系xOy中，点在轴正半轴上，点C在y轴正半轴上．
①如图1，正方形OABC的边长为2，求以O为顶点的对角抛物线；
②如图2，在平面直角坐标系xOy中，正方形OABC的边长为a，其以O为顶点的对角抛物线的解析式为y=$\frac{1}{4}$x²，求a的值；         
 （2）如图3，正方形ABCD的边长为4，且点A的坐标为（3，2），正方形的四条对角抛物线在正方形ABCD内分别交于点M、P、N、Q，直接写出四边形MPNQ的形状和四边形MPNQ的对角线的交点坐标．

Answer 1

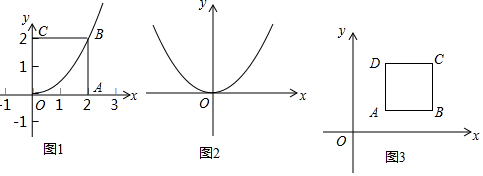
分析 （1）①设O为顶点的抛物线的解析式为y=ax²，把B（2，2）代入即可解决问题．
②设B（a，a）．代入y=$\frac{1}{4}$x²求出a即可解决问题．
（2）如图3中，结论：四边形MPNQ是菱形，对角线的交点坐标为（5，4）．求出A、B、C、D的顶点的对角抛物线，利用方程组求出M、P、N、Q的坐标即可解决问题．

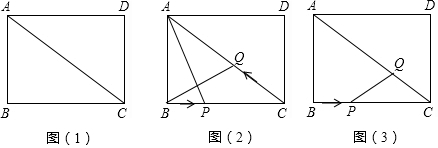
解答 解：（1）①如图1中，设O为顶点的抛物线的解析式为y=ax²，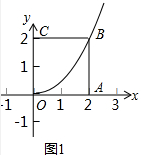

∵过B（2，2），
∴2=4a，
∴a=$\frac{1}{2}$，
∴所求的抛物线的解析式为y=$\frac{1}{2}$x²．

②如图2中，设B（a，a）．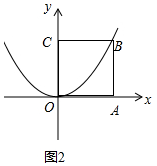

则有a=$\frac{1}{4}$a²，解得a=4或0（舍弃），
∴B（4，4），
∴OA=4，
∴正方形的边长为4．

（2）如图3中，结论：四边形MPNQ是菱形，对角线的交点坐标为（5，4）．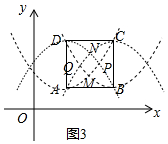

理由：∵正方形ABCD的边长为4，A（3，2），
∴B（7，2），C（7，6），D（3，6），
∴以A为顶点的对角抛物线为y=$\frac{1}{4}$（x-3）²+2，
以B为顶点的对角抛物线为y=$\frac{1}{4}$（x-7）²+2，
以C为顶点的对角抛物线为y=-$\frac{1}{4}$（x-7）²+6，
以D为顶点的对角抛物线为y=-$\frac{1}{4}$（x-3）²+6，
由$\left\{\begin{array}{l}{y=\frac{1}{4}（x-3）^{2}+2}\\{y=\frac{1}{4}（x-7）^{2}+2}\end{array}\right.$可得M（5，3），
由$\left\{\begin{array}{l}{y=-\frac{1}{4}（x-7）^{2}+6}\\{y=-\frac{1}{2}（x-3）^{2}+6}\end{array}\right.$可得N（5，5），
由$\left\{\begin{array}{l}{y=\frac{1}{4}（x-3）^{2}+2}\\{Y=-\frac{1}{4}（x-3）^{2}+6}\end{array}\right.$可得P（3+2$\sqrt{2}$，4），
由$\left\{\begin{array}{l}{y=\frac{1}{4}（x-7）^{2}+2}\\{y=-\frac{1}{4}（x-7）^{2}+6}\end{array}\right.$可得Q（7-2$\sqrt{2}$，4），
∴PM=$\sqrt{（2\sqrt{2}-2）^{2}+{1}^{2}}$，
PN=$\sqrt{（2\sqrt{2}-2）^{2}+{1}^{2}}$，
QN=$\sqrt{（2\sqrt{2}-2）^{2}+{1}^{2}}$，
QM=$\sqrt{（2\sqrt{2}-2）^{2}+{1}^{2}}$，
∴PM=PN=QN=QM，
∴四边形MPNQ是菱形，对角线的交点坐标为（5，5）．

点评 本题考查二次函数综合题，待定系数法、二元二次方程组、两点之间的距离公式、菱形的判定等知识，解题的关键是灵活应用待定系数法确定函数解析式，学会利用方程组求两个函数图象的交点坐标，属于中考压轴题．